
【题目】在①![]() ,
,![]() ,②
,②![]() ,
,![]() ,③
,③![]() ,
,![]() 三个条件中任选一个补充在下面问题中,并加以解答.
三个条件中任选一个补充在下面问题中,并加以解答.
已知![]() 的内角A,B,C的对边分别为a,b,c,若
的内角A,B,C的对边分别为a,b,c,若![]() ,______,求
,______,求![]() 的面积S.
的面积S.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】点![]() 与定点
与定点![]() 的距离和它到直线
的距离和它到直线![]() 的距离的比是常数
的距离的比是常数![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 的中点为
的中点为![]() ,
,![]() ,
,![]() 两点为曲线
两点为曲线![]() 上关于原点
上关于原点![]() 对称的两点,且
对称的两点,且![]() (
(![]() ),求四边形
),求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为常数,
为常数,![]() 为自然对数的底数,)
为自然对数的底数,)
(1)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值集合,
的取值集合,
(2)已知正数![]() 满足:存在
满足:存在![]() ,使不等式
,使不等式![]() 成立.
成立.
①求![]() 的取值集合;
的取值集合;
②试比较![]() 与
与![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
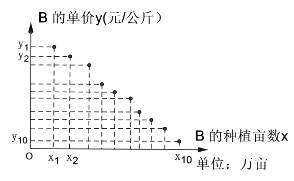
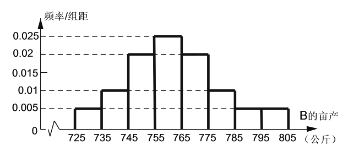
【题目】某地种植常规稻A和杂交稻B,常规稻A的亩产稳定为500公斤,今年单价为3.50元/公斤,估计明年单价不变的可能性为10%,变为3.60元/公斤的可能性为60%,变为3.70元/公斤的可能性为30%.统计杂交稻B的亩产数据,得到亩产的频率分布直方图如下;统计近10年来杂交稻B的单价(单位:元/公斤)与种植亩数(单位:万亩)的关系,得到的10组数据记为![]() ,并得到散点图如下,参考数据见下.
,并得到散点图如下,参考数据见下.
(1)估计明年常规稻A的单价平均值;
(2)在频率分布直方图中,各组的取值按中间值来计算,求杂交稻B的亩产平均值;以频率作为概率,预计将来三年中至少有二年,杂交稻B的亩产超过765公斤的概率;
(3)判断杂交稻B的单价y(单位:元/公斤)与种植亩数x(单位:万亩)是否线性相关?若相关,试根据以下的参考数据求出y关于x的线性回归方程;调查得知明年此地杂交稻B的种植亩数预计为2万亩.若在常规稻A和杂交稻B中选择,明年种植哪种水稻收入更高?
统计参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
附:线性回归方程![]() ,
,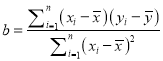 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年6月14日,世界杯足球赛在俄罗斯拉开帷幕,世界杯给俄罗斯经济带来了一定的增长,某纪念商品店的销售人员为了统计世界杯足球赛期间商品的销售情况,随机抽查了该商品商店某天200名顾客的消费金额情况,得到如图频率分布表:将消费顾客超过4万卢布的顾客定义为”足球迷”,消费金额不超过4万卢布的顾客定义为“非足球迷”。
消费金额/万卢布 |
|
|
|
|
|
| 合计 |
顾客人数 | 9 | 31 | 36 | 44 | 62 | 18 | 200 |
(1)求这200名顾客消费金额的中位数与平均数(同一组中的消费金额用该组的中点值作代表;
(2)该纪念品商店的销售人员为了进一步了解这200名顾客喜欢纪念品的类型,采用分层抽样的方法从“非足球迷”,“足球迷”中选取5人,再从这5人中随机选取3人进行问卷调查,则选取的3人中“非足球迷”人数的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥A﹣BCD中,△ABD和△ACD是边长为2的等边三角形,![]() ,O、E分别是BC、AC的中点.
,O、E分别是BC、AC的中点.
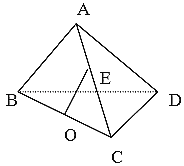
(1)求证:OE∥平面ABD;
(2)求证:平面ABC⊥平面BCD;
(3)求三棱锥A﹣BCD的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆与双曲线![]() 有相同的焦点坐标,且点
有相同的焦点坐标,且点![]() 在椭圆上.
在椭圆上.
(1)求椭圆的标准方程;
(2)设A、B分别是椭圆的左、右顶点,动点M满足![]() ,垂足为B,连接AM交椭圆于点P(异于A),则是否存在定点T,使得以线段MP为直径的圆恒过直线BP与MT的交点Q,若存在,求出点T的坐标;若不存在,请说明理由.
,垂足为B,连接AM交椭圆于点P(异于A),则是否存在定点T,使得以线段MP为直径的圆恒过直线BP与MT的交点Q,若存在,求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为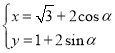 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() ,(t为参数),在以原点为极点,x轴正半轴为极轴的极坐标中,曲线
,(t为参数),在以原点为极点,x轴正半轴为极轴的极坐标中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将![]() 与
与![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)若曲线![]() 与
与![]() 的公共点都在
的公共点都在![]() 上,
上,![]() ,求r.
,求r.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com