
分析 (1)由已有可得直线AB过点P(-1,0)设直线AB的方程为:x=my-1,$A(\frac{{{y_1}^2}}{4},{y_1})$、$B(\frac{{{y_2}^2}}{4},{y_2})$,联立直线与抛物线方程,由韦达定理和向量数量积的定义,可得答案;
(2)设$C(\frac{{{y_0}^2}}{4},{y_0})$(y0>0),利用导数法,求出l的方程,解得答案.
解答 解:(1)∵抛物线y2=4x的焦点为F为(1,0),
准线与x轴的交点P为(-1,0),
故直线AB过点P(-1,0)
∴设直线AB的方程为:x=my-1,$A(\frac{{{y_1}^2}}{4},{y_1})$、$B(\frac{{{y_2}^2}}{4},{y_2})$
由$\left\{\begin{array}{l}x=my-1\\{y^2}=4x\end{array}\right.$得y2-4my+4=0,则y1•y2=4,
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{{{y_1}^2}}{4}•\frac{{{y_2}^2}}{4}+{y_1}•{y_2}=5$
证明:(2)设$C(\frac{{{y_0}^2}}{4},{y_0})$(y0>0),
∵抛物线y2=4x在第一象限的方程可化为函数$y=2\sqrt{x}$,$y'=\frac{1}{{\sqrt{x}}}$,
∴直线l的斜率为$\frac{2}{y_0}$,直线l的方程为:$y=\frac{2}{y_0}x+\frac{y_0}{2}$
过C点作抛物线准线的垂线,垂足为D(-1,y0),根据抛物线定义:|CF|=|CD|
线段DF的垂直平分线方程为:$y=\frac{2}{y_0}x+\frac{y_0}{2}$与直线l重合
∴F关于直线l的对称点在抛物线的准线上.
点评 本题考查的知识点是抛物线的简单性质,熟练掌握抛物线的性质是解答的关键.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}})$ | B. | $({0,\frac{{\sqrt{2}}}{2}})$ | C. | $({\frac{1}{2},1})$ | D. | $({\frac{{\sqrt{2}}}{2},1})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{{3\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
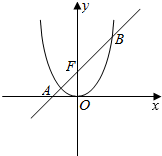 如图,已知抛物线C:x2=2py(0<p<4),其上一点M(4,y0)到其焦点F的距离为5,过焦点F的直线l与抛物线C交于A,B左、右两点.
如图,已知抛物线C:x2=2py(0<p<4),其上一点M(4,y0)到其焦点F的距离为5,过焦点F的直线l与抛物线C交于A,B左、右两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\sqrt{2}$-1) | B. | ($\frac{\sqrt{2}}{2}$,1) | C. | (0,$\frac{\sqrt{2}}{2}$) | D. | ($\sqrt{2}$-1,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com