
【题目】某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题: 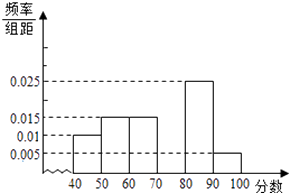
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率.
【答案】
(1)解:第一小组的频率为0.010×10=0.1,第二小组的频率为0.015×10=0.15,第三小组的频率为0.015×10=0.15,第五小组的频率为0.025×10=0.25,第六小组的频率为0.005×10=0.05,所以第四小组的频率为1﹣0.1﹣0.15﹣0.15﹣0.25﹣0.05=0.3.
频率/组距=0.3÷10=0.03,故频率分布直方图如图
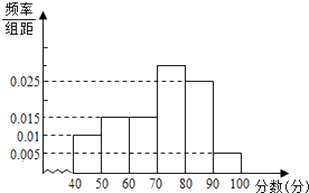
(2)解:平均分超过60分的频率为0.15+0.25+0.05+0.3=0.75,所以估计这次考试的及格率为75%.
第一组人数0.10×60=6,第二组人数0.15×60=9,第三组人数0.15×60=9,第四组人数0.3×60=18,第五组人数0.25×60=15,第六组人数0.05×60=3,
所以平均分为 ![]() =71
=71
(3)解:成绩在[40,50)的有6人,在[90,100]的有3人,从中选两人有 ![]() ,他们在同一分数段的有
,他们在同一分数段的有 ![]() ,
,
所以他们在同一分数段的概率是 ![]() .
.
【解析】(1)根据频率直方图的性质求第四小组的频率.(2)利用样本进行总体估计.(3)根据古典概型的概率公式求概率.
【考点精析】通过灵活运用频率分布直方图和用样本的频率分布估计总体分布,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;样本数据的频率分布表和频率分布直方图,是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律,它可以让我们更清楚的看到整个样本数据的频率分布情况,并由此估计总体的分布情况即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】园林管理处拟在公园某区域规划建设一半径为![]() 米圆心角为
米圆心角为![]() (弧度)的扇形景观水池,其中
(弧度)的扇形景观水池,其中![]() 为扇形
为扇形![]() 的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过
的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过![]() 万元,水池造价为每平方米
万元,水池造价为每平方米![]() 元,步道造价为每米
元,步道造价为每米![]() 元.
元.
(1)当![]() 和
和![]() 分别为多少时,可使广场面积最大,并求出最大值;
分别为多少时,可使广场面积最大,并求出最大值;
(2)若要求步道长为![]() 米,则可设计出水池最大面积是多少.
米,则可设计出水池最大面积是多少.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点P的坐标为(x﹣3,y﹣2).
(1)在一个盒子中,放有标号为1,2,3的三张卡片,现在从盒子中随机取出一张卡片,记下标号后把卡片放回盒中,再从盒子中随机取出一张卡片记下标号,记先后两次抽取卡片的标号分别为x、y,求点P在第二象限的概率;
(2)若利用计算机随机在区间[0,3]上先后取两个数分别记为x、y,求点P在第三象限的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2).
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ–3σ,μ+3σ)之外的零件数,求P(X≥1)及X的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在(μ–3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
,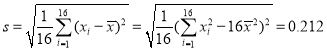 ,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计μ和σ(精确到0.01).
之外的数据,用剩下的数据估计μ和σ(精确到0.01).
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ–3σ<Z<μ+3σ)=0.997 4,0.997 416≈0.959 2,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形, 且∠DAB=90°,∠ABC=45°,CB= ![]() ,AB=2,PA=1
,AB=2,PA=1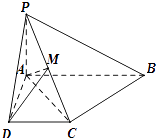
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
(3)若M是PC的中点,求三棱锥C﹣MAD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC= ![]() .
. 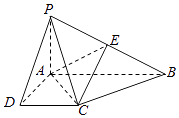
(1)求证:平面PAD⊥平面PCD;
(2)试在棱PB上确定一点E,使截面AEC把该几何体分成的两部分PDCEA与EACB的体积比为2:1;
(3)在(2)的条件下,求二面角E﹣AC﹣P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD是平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EB= ![]() ,EF=1,BC=
,EF=1,BC= ![]() ,且M是BD的中点..
,且M是BD的中点.. 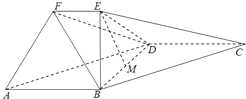
(1)求证:EM∥平面ADF;
(2)求直线DF和平面ABCD所成角的正切值;
(3)求二面角D﹣AF﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x,y满足不等式组  ,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为( )
,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为( )
A.[﹣1,2]
B.[﹣2,1]
C.[﹣3,﹣2]
D.[﹣3,1]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com