
【题目】上海市普通高中学业水平等级考成绩共分为五等十一级,各等级换算成分数如表所示:
等级 |
| A |
| B |
|
| C |
|
| D | E |
分数 | 70 | 67 | 64 | 61 | 58 | 55 | 52 | 49 | 46 | 43 | 40 |
上海某高中2018届高三![]() 班选考物理学业水平等级考的学生中,有5人取得
班选考物理学业水平等级考的学生中,有5人取得![]() 成绩,其他人的成绩至少是B级及以上,平均分是64分,这个班级选考物理学业水平等级考的人数至少为______人
成绩,其他人的成绩至少是B级及以上,平均分是64分,这个班级选考物理学业水平等级考的人数至少为______人![]()
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中有如下正确结论:
中有如下正确结论:![]() 为曲线
为曲线![]() (
(![]() 、
、![]() 为非零实数,且不同时为负)上一点,则过点
为非零实数,且不同时为负)上一点,则过点![]() 的切线方程为
的切线方程为![]() .
.
(1)已知![]() 为椭圆
为椭圆![]() 上一点,
上一点,![]() 为过点
为过点![]() 的椭圆的切线,若直线
的椭圆的切线,若直线![]() 与直线
与直线![]() 的斜率分别为
的斜率分别为![]() 与
与![]() ,求证:
,求证:![]() 为定值;
为定值;
(2)过椭圆![]() 上一点
上一点![]() 引椭圆
引椭圆![]() 的切线,与
的切线,与![]() 轴交于点
轴交于点![]() .若
.若![]() 为正三角形,求椭圆
为正三角形,求椭圆![]() 的方程;
的方程;
(3)求与圆![]() 及(2)中的椭圆
及(2)中的椭圆![]() 均相切的直线
均相切的直线![]() 与坐标轴围成的三角形的面积的取值范围.
与坐标轴围成的三角形的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x,y的方程x2+y2﹣4x+4y+m=0表示一个圆.
(1)求实数m的取值范围;
(2)若m=4,过点P(0,2)的直线l与圆相切,求出直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆P恒过定点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆P圆心的轨迹M的方程;
(Ⅱ)正方形ABCD中,一条边AB在直线y=x+4上,另外两点C、D在轨迹M上,求正方形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() 是椭圆E的右焦点,直线AF的斜率为2,O为坐标原点.
是椭圆E的右焦点,直线AF的斜率为2,O为坐标原点.
(1)求E的方程;
(2)设过点![]() 且斜率为k的直线
且斜率为k的直线![]() 与椭圆E交于不同的两M、N,且
与椭圆E交于不同的两M、N,且![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,四点
,四点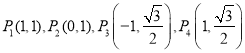 中恰有三点在椭圆上.
中恰有三点在椭圆上.
(1)求椭圆C的方程
(2)椭圆C上是否存在不同的两点M,N关于直线![]() 对称?若存在,请求出直线MN的方程,若不存在,请说明理由.
对称?若存在,请求出直线MN的方程,若不存在,请说明理由.
(3)设直线l不经过点![]() 且与C相交于A,B两点,若直线
且与C相交于A,B两点,若直线![]() 与直线
与直线![]() 的斜率之和为1,求证直线l必过定点,并求出这个定点坐标.
的斜率之和为1,求证直线l必过定点,并求出这个定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S-ABCD的底面是边长为1的正方形,则棱SB垂直于底面.
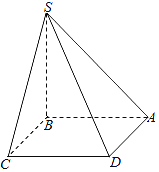
(1)求证:平面SBD⊥平面SAC;
(2)若SA与平面SCD所成角的正弦值为![]() ,求SB的长.
,求SB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A. 甲地:总体均值为3,中位数为4 B. 乙地:总体均值为1,总体方差大于0
C. 丙地:中位数为2,众数为3 D. 丁地:总体均值为2,总体方差为3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)求圆![]() 的直角坐标方程及弦
的直角坐标方程及弦![]() 的长;
的长;
(2)动点![]() 在圆
在圆![]() 上(不与
上(不与![]() ,
, ![]() 重合),试求
重合),试求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com