
【题目】如图1,在梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD,四边形ABEF是矩形,将矩形ABEF沿AB折起到四边形ABE1F1的位置,使平面ABE1F1⊥平面ABCD,M为AF1的中点,如图2.
(1)求证:BE1⊥DC;
(2)求证:DM∥平面BCE1;
(3)判断直线CD与ME1的位置关系,并说明理由.

【答案】(1)见解析;(2)见解析.(3)相交,理由详见解析
【解析】试题分析:(1)由面面垂直性质定理得BE1⊥平面ABCD,即得BE1⊥DC;(2)根据AM∥BE1,AD∥BC,可根据线面平行判定定理得线面平行,再根据面面平行判定定理得面面平行,即得结论(3)取BC的中点P,CE1的中点Q,易得MQ∥CD,因此相交
试题解析:(1)证明 因为四边形ABE1F1为矩形,
所以BE1⊥AB.
因为平面ABCD⊥平面ABE1F1,
且平面ABCD∩平面ABE1F1=AB,
BE1平面ABE1F1,
所以BE1⊥平面ABCD.
因为DC平面ABCD,
所以BE1⊥DC.
(2)证明 因为四边形ABE1F1为矩形,
所以AM∥BE1.
因为AD∥BC,AD∩AM=A,BC∩BE1=B,
AD平面ADM,AM平面ADM,
BC平面BCE1,BE1平面BCE1,
所以平面ADM∥平面BCE1.
因为DM平面ADM,
所以DM∥平面BCE1.
(3)解 直线CD与ME1相交,理由如下:
取BC的中点P,CE1的中点Q,连接AP,PQ,QM,
所以PQ∥BE1,且PQ=![]() BE1.
BE1.
在矩形ABE1F1中,M为AF1的中点,
所以AM∥BE1,且AM=![]() BE1,
BE1,
所以PQ∥AM,且PQ=AM.
所以四边形APQM为平行四边形,
所以MQ∥AP,MQ=AP.

因为四边形ABCD为梯形,P为BC的中点,BC=2AD,
所以AD∥PC,AD=PC,
所以四边形ADCP为平行四边形.
所以CD∥AP且CD=AP.
所以CD∥MQ且CD=MQ.
所以四边形CDMQ是平行四边形.
所以DM∥CQ,即DM∥CE1.
因为DM≠CE1,
所以四边形DME1C是以DM,CE1为底边的梯形,
所以直线CD与ME1相交.
点睛:立体几何中折叠问题,要注重折叠前后垂直关系的变化,不变的垂直关系是解决问题的关键条件.


 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若函数![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2)设函数![]() ,若对任意的
,若对任意的![]() ,都有
,都有![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)设![]() ,点
,点![]() 是函数
是函数![]() 与
与![]() 的一个交点,且函数
的一个交点,且函数![]() 与
与![]() 在点
在点![]() 处的切线互相垂直,求证:存在唯一的
处的切线互相垂直,求证:存在唯一的![]() 满足题意,且
满足题意,且![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的运动方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
步数 性别 | 0-2000 | 2001-5000 | 5001-8000 | 8001-10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
附: 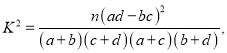
(1)已知某人一天的走路步数超过8000步被系统评定为“积极型”,否则为“懈怠型”,根据题意完成下面的 积极型 懈怠型 总计 男 女 总计 (2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (其中e是自然对数的底数,常数a>0).
(其中e是自然对数的底数,常数a>0).
(1)当a=1时,求曲线在(0,f(0))处的切线方程;
(2)若存在实数x∈(a,2],使得不等式f(x)≤e2成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
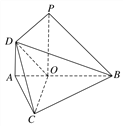
【题目】如图,在△ABC中,∠ABC=45°,点O在AB上,且OB=OC=![]() AB,PO⊥平面ABC,DA∥PO,DA=AO=
AB,PO⊥平面ABC,DA∥PO,DA=AO=![]() PO.
PO.
(1)求证:PB∥平面COD;
(2)求二面角O-CD-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
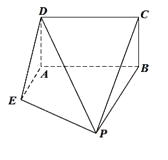
【题目】如图,已知矩形![]() 所在平面垂直于直角梯形
所在平面垂直于直角梯形![]() 所在平面于直线
所在平面于直线![]() ,且
,且![]() ,
, ![]() 且
且![]() ∥
∥![]() .
.
(Ⅰ)设点![]() 为棱
为棱![]() 中点,求证:
中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某单位的食堂中,食堂每天以10元/斤的价格购进米粉,然后以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂购进了80斤米粉,以![]() (斤)(其中
(斤)(其中![]() )表示米粉的需求量,
)表示米粉的需求量, ![]() (元)表示利润.
(元)表示利润.
(1)估计该天食堂利润不少于760元的概率;
(2)在直方图的需求量分组中,以区间中间值作为该区间的需求量,以需求量落入该区间的频率作为需求量在该区间的概率,求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中点在原点,焦点在
的中点在原点,焦点在![]() 轴上,离心率
轴上,离心率![]() ,以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为
,以两个焦点和短轴的两个端点为顶点的四边形的周长为8,面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点![]() 的两条直线
的两条直线![]() ,
, ![]() ,交椭圆
,交椭圆![]() 于
于![]() ,
, ![]() ,
, ![]() ,
, ![]() 四点,若
四点,若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com