
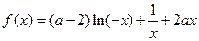 (
(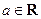 ).
).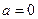 时,求
时,求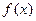 的极值;
的极值;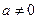 时,求
时,求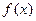 的单调区间.
的单调区间. 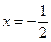 时,
时,  取得极大值为
取得极大值为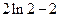 .
.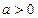 时,
时, 的增区间为
的增区间为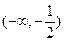 ,减区间为
,减区间为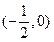 ;
;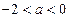 时,
时, 的增区间为
的增区间为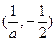 ,减区间为
,减区间为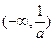 ,
,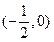 ;
;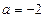 时,
时, 的减区间为
的减区间为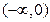 ,无增区间;
,无增区间;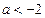 时,
时, 的增区间为
的增区间为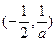 ,减区间为
,减区间为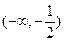 ,
,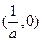 .
. 的定义域为
的定义域为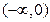 .
.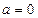 时,
时,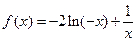 ,
,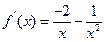
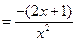 .
.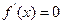 ,解得
,解得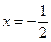 .
.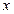 变化时,
变化时,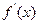 与
与 的变化情况如下表:
的变化情况如下表: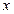 | 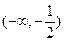 | 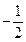 | 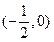 |
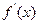 | 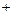 | 0 | 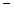 |
 | 单调递增 | 极大值 | 单调递减 |
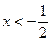 时,
时,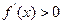 ;当
;当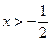 时,
时,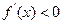 .
.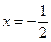 时,
时,  取得极大值为
取得极大值为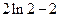 .-------------------5分
.-------------------5分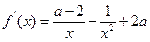
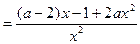
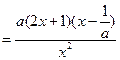
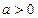 ,令
,令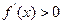 ,解得:
,解得: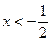 ;令
;令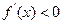 ,解得:
,解得: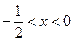 .
.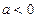 ,①当
,①当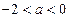 时,
时,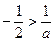
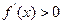 ,解得:
,解得: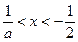 ;
;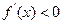 ,解得:
,解得: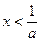 或
或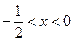 .
.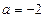 时,
时,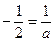 ,
,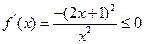
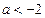 时,
时,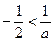
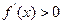 ,解得:
,解得: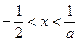 ;
;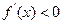 ,解得:
,解得: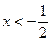 或
或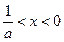 .
.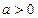 时,
时, 的增区间为
的增区间为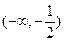 ,减区间为
,减区间为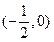 ;
;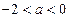 时,
时, 的增区间为
的增区间为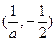 ,减区间为
,减区间为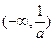 ,
,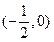 ;
;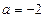 时,
时, 的减区间为
的减区间为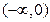 ,无增区间;
,无增区间;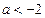 时,
时, 的增区间为
的增区间为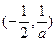 ,减区间为
,减区间为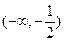 ,
,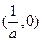 .
.

科目:高中数学 来源:不详 题型:解答题
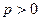 ,动点
,动点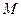 到定点
到定点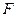
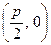 的距离比
的距离比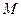 到定直线
到定直线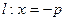 的距离小
的距离小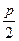 .
.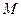 的轨迹
的轨迹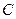 的方程;
的方程;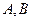 是轨迹
是轨迹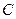 上异于原点
上异于原点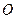 的两个不同点,
的两个不同点,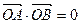 ,求
,求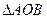 面积的最小值;
面积的最小值;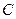 上是否存在两点
上是否存在两点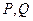 关于直线
关于直线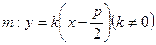 对称?若存在,求出直线
对称?若存在,求出直线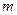 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
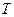 :
: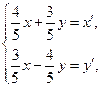 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点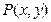 变换到这一平面上的一点
变换到这一平面上的一点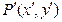 .
.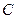 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在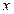 轴上,且焦距为
轴上,且焦距为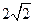 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆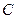 的标准方程,并求出其两个焦点
的标准方程,并求出其两个焦点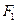 、
、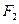 经变换公式
经变换公式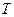 变换后得到的点
变换后得到的点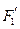 和
和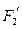 的坐标;
的坐标;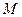 上一点
上一点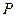 经变换公式
经变换公式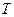 变换后得到的点
变换后得到的点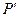 与点
与点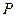 重合,则称点
重合,则称点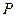 是曲线
是曲线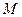 在变换
在变换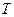 下的不动点. 求(1)中的椭圆
下的不动点. 求(1)中的椭圆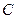 在变换
在变换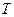 下的所有不动点的坐标;
下的所有不动点的坐标;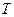 下的不动点的存在情况和个数.
下的不动点的存在情况和个数. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com