
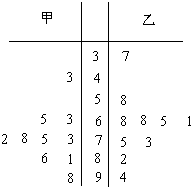
 PM2.5��ָ���������п�������ѧ����ֱ��С�ڻ����2.5 �Ŀ����һ�������PM2.5Ũ��Խ�ߣ��ʹ���������ȾԽ���أ���ͼ��ʾ�ľ�Ҷͼ��ʾ����ij�����ס����������վij10����ÿ���PM2.5Ũ�ȶ�������λ����g/m3����������˵����ȷ���ǣ�������
PM2.5��ָ���������п�������ѧ����ֱ��С�ڻ����2.5 �Ŀ����һ�������PM2.5Ũ��Խ�ߣ��ʹ���������ȾԽ���أ���ͼ��ʾ�ľ�Ҷͼ��ʾ����ij�����ס����������վij10����ÿ���PM2.5Ũ�ȶ�������λ����g/m3����������˵����ȷ���ǣ�������| A�� | ��10 ���ڼס��Ҽ��վ�����ļ������ | |
| B�� | ��10 ���ڼס��Ҽ��վ��������λ���У��ҵĽϴ� | |
| C�� | ��10 �����Ҽ��վ��������������λ����� | |
| D�� | ��10 ���ڼס��Ҽ��վ������ƽ������� |
���� ���ݾ�Ҷͼ�е����ݷֲ����ֱ�������ҵļ����λ����������ƽ�����Ƚϼ��ɣ�
��� �⣺���ݾ�Ҷͼ�е����ݿ�֪��
��l0���ڼס�����Ϊ55����λ��Ϊ74��ƽ����Ϊ73.4��
��l0�����ҡ�����Ϊ57����λ��Ϊ68������Ϊ68��ƽ����Ϊ68.1��
ͨ�����ϵ����ݷ�������֪C��ȷ��
��ѡ��C��
���� ���⿼�龥Ҷͼ��ʶ����жϣ����ݾ�Ҷͼ�����ݷֲ����������ȷ�������λ����������ƽ������С���Ƚϻ�����


 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д� �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 120 | B�� | 240 | C�� | 360 | D�� | 480 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��1����f��3����f��5�� | B�� | f��1����f��5����f��3�� | C�� | f��3����f��1����f��5�� | D�� | f��3����f��5����f��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com