
分析 (1)利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性以及它的图象的对称性,求得f(x)的最小正周期及其图象的对称中心.
(2)利用正弦函数的单调性,求得函数f(x)的单调递增区间.
解答 解:(1)$f(x)=\frac{1}{2}sin2x+\frac{{\sqrt{3}}}{2}cos2x-\sqrt{3}cos2x$=$\frac{1}{2}sin2x-\frac{{\sqrt{3}}}{2}cos2x$=$sin({2x-\frac{π}{3}})$,
所以f(x)的最小正周期为$T=\frac{2π}{2}=π$.
令$2x-\frac{π}{3}=kπ({k∈Z})$,求得x=$\frac{kπ}{2}$+$\frac{π}{6}$,可得函数的图象对称中心为$({\frac{kπ}{2}+\frac{π}{6},0})({k∈Z})$.
(2)令$2kπ-\frac{π}{2}≤2x-\frac{π}{3}≤2kπ+\frac{π}{2}({k∈Z})$,解得$kπ-\frac{π}{12}≤x≤kπ+\frac{5π}{12}({k∈Z})$,
所以f(x)的单调递增区间为$[{kπ-\frac{π}{12},kπ+\frac{5π}{12}}]({k∈Z})$.
点评 本题主要考查三角恒等变换,正弦函数的周期性和单调性,以及它的图象的对称性,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $-\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
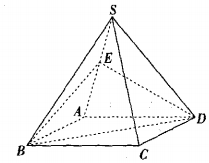 如图,四棱锥S-ABCD中,底面ABCD为平行四边形,E是SA的上一点,当点E满足条件SE=EA,时,SC∥平面EBD,写出条件并加以证明.
如图,四棱锥S-ABCD中,底面ABCD为平行四边形,E是SA的上一点,当点E满足条件SE=EA,时,SC∥平面EBD,写出条件并加以证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com