
【题目】已知棱长为![]() 的正方体
的正方体![]() 中,
中,![]() 分别为棱
分别为棱![]() 和
和![]() 的中点.
的中点.
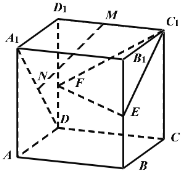
(1)证明:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)证法一:连结![]() 交
交![]() 于点
于点![]() ,利用平几知识证四边形
,利用平几知识证四边形![]() 为平行四边形,再根据线面平行判定定理得结果;证法二:取
为平行四边形,再根据线面平行判定定理得结果;证法二:取![]() 中点
中点![]() ,利用平几知识证
,利用平几知识证![]() ∥
∥![]()
![]() ,再根据线面平行判定定理得结果;
,再根据线面平行判定定理得结果;
(2))解法一与解法二,利用等体积法求点到直线距离.
(1)证法一:如图连结![]() 交
交![]() 于点
于点![]() ,则点
,则点![]() 为
为![]() 的中点,连结
的中点,连结![]() ,
,![]()
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() 为
为![]() 的中位线,∴
的中位线,∴![]() ∥
∥![]() ,
,![]()
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ∥
∥![]() ,
,![]() ,∴四边形
,∴四边形![]() 为平行四边形
为平行四边形
∴![]() ∥
∥![]() ,∵
,∵![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() ∥平面
∥平面![]() .
.
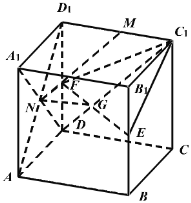
证法二:如图取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,因为正方体
,因为正方体![]() ,
,
![]() 分别为
分别为![]() 中点,所以可得四边形
中点,所以可得四边形![]() 和四边形
和四边形![]() 均为平行四边
均为平行四边
形,所以![]() ∥
∥![]() ∥
∥![]() ,所以平面
,所以平面![]() 即为平行四边形
即为平行四边形![]() 所在平面,因为
所在平面,因为![]()
为![]() 的中点,所以也为
的中点,所以也为![]() 中点,且
中点,且![]() 为
为![]() 中点,所以
中点,所以![]() ∥
∥![]()
![]() ,∴
,∴![]() ∥平面
∥平面![]() .
.

(2)解法一:延长![]() 到点
到点![]() ,使得
,使得![]() ,连结
,连结![]() ,则
,则![]() ∥平面
∥平面![]() ,
,
则![]() 到平面
到平面![]() 的距离即
的距离即![]() 到平面
到平面![]() 的距离,
的距离,![]() ,点
,点![]() 到平面
到平面![]() 的距
的距
离为![]() ,
,![]() ,
,

设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则
,则![]() ,即
,即![]()
可得![]() ,即点
,即点![]() 到平面
到平面![]() 的距离为
的距离为![]()
解法二:由证法二知点![]() 到平面
到平面![]() 的距离为
的距离为![]() 到平面
到平面![]() 的距离,所以
的距离,所以![]() ,
,
且![]() ,
,![]() ,所以
,所以![]() 到平面
到平面![]() 的距离为
的距离为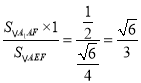 .
.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】某中学高二年级组织外出参加学业水平考试,出行方式为:乘坐学校定制公交或自行打车前往,大数据分析显示,当![]() 的学生选择自行打车,自行打车的平均时间为
的学生选择自行打车,自行打车的平均时间为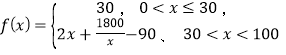 (单位:分钟) ,而乘坐定制公交的平均时间不受
(单位:分钟) ,而乘坐定制公交的平均时间不受![]() 影响,恒为40分钟,试根据上述分析结果回答下列问题:
影响,恒为40分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?
在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?
(2)求该校学生参加考试平均时间![]() 的表达式:讨论
的表达式:讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,以下结论:
上的动点,以下结论:
①![]() 平面
平面![]() ;
;
②![]() ;
;
③三棱锥![]() ,体积不变;
,体积不变;
④![]() 为
为![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大.
所成角最大.
其中正确的序号为( )
A.①④B.②④C.①②③D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() 交于M,抛物线C的焦点为F,且
交于M,抛物线C的焦点为F,且![]() .
.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设点Q是抛物线C上的动点,点D,E在y轴上,圆![]() 内切于三角形
内切于三角形![]() ,求三角形
,求三角形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的焦点坐标为![]() ,
,![]() ,过
,过![]() 垂直于长轴的直线交椭圆于
垂直于长轴的直线交椭圆于![]() 、
、![]() 两点,且
两点,且![]() .
.

(1)求椭圆的方程;
(2)过![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 、
、![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 是一直角梯形,
是一直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 底面
底面![]() .
.
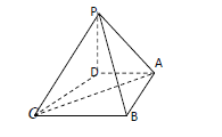
(1)在线段![]() 上是否存在一点F,使得
上是否存在一点F,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,试说明理由;
的值;若不存在,试说明理由;
(2)在(1)的条件下,若![]() 与
与![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》是中国古代重要的数学著作,其记载的“日月历法”曰:“阴阳之数,日月之法,十九岁为一章,四章为一部,部七十六岁,二十部为一遂,遂千百五二十岁,….生数皆终,万物复苏,天以更元作纪历”,某老年公寓住有20位老人,他们的年龄(都为正整数)之和恰好为一遂,其中年长者已是奔百之龄(年龄介于90至100),其余19人的年龄依次相差一岁,则年长者的年龄为( )
A.94B.95C.96D.98
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com