解:(1)由

∥

得:1-2cos2A=2

sin

cos

,即

,
所以
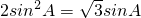
,
又A为锐角,∴
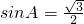
,

,(3分)
而a
2-c
2=b
2-mbc可以变形为
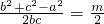
即
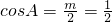
,所以m=1;(6分)
(2)由(1)知:

,
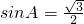
,
又
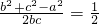
,
所以bc=b
2+c
2-a
2≥2bc-a
2即bc≤a
2,(9分)
故

,
当且仅当
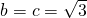
时,△ABC面积的最大值是

.(12分)
分析:(1)由向量平行时,向量的坐标对应成比例得到一个关系式,利用二倍角的正弦、余弦函数公式化简,由sinA不为0,得到sinA的值,又A为锐角,利用同角三角函数间的基本关系求出cosA的值,利用余弦定理表示出cosA,把已知的等式代入即可表示出cosA,由cosA的值列出关于m的方程,求出方程的解即可得到m的值;
(2)由(1)中求出的sinA和cosA的值,根据
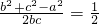
,解出bc,利用基本不等式求出bc的最大值,然后利用三角形的面积公式表示出三角形ABC的面积,把bc的最大值及sinA的值代入即可求出三角形ABC面积的最大值.
点评:此题考查了三角函数的恒等变换,余弦定理及三角形的面积公式,要求学生掌握平面向量的数量积的运算法则,二倍角正弦、余弦函数公式,同角三角函数间的基本关系,以及基本不等式.灵活利用基本不等式求出bc的最大值是第二问求三角形面积最大的关键.

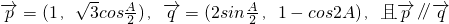 .
. ,求△ABC面积的最大值.
,求△ABC面积的最大值. ∥
∥ 得:1-2cos2A=2
得:1-2cos2A=2 sin
sin cos
cos ,即
,即 ,
,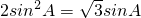 ,
,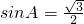 ,
, ,(3分)
,(3分)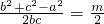
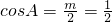 ,所以m=1;(6分)
,所以m=1;(6分) ,
,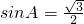 ,
,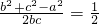 ,
, ,
,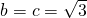 时,△ABC面积的最大值是
时,△ABC面积的最大值是 .(12分)
.(12分)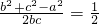 ,解出bc,利用基本不等式求出bc的最大值,然后利用三角形的面积公式表示出三角形ABC的面积,把bc的最大值及sinA的值代入即可求出三角形ABC面积的最大值.
,解出bc,利用基本不等式求出bc的最大值,然后利用三角形的面积公式表示出三角形ABC的面积,把bc的最大值及sinA的值代入即可求出三角形ABC面积的最大值.

 名校课堂系列答案
名校课堂系列答案