
【题目】某芯片公司为制定下一年的研发投入计划,需了解年研发资金投入量![]() (单位:亿元)对年销售额
(单位:亿元)对年销售额![]() (单位:亿元)的影响.该公司对历史数据进行对比分析,建立了两个函数模型:①
(单位:亿元)的影响.该公司对历史数据进行对比分析,建立了两个函数模型:①![]() ,②
,②![]() ,其中
,其中![]() 均为常数,
均为常数,![]() 为自然对数的底数.
为自然对数的底数.

现该公司收集了近12年的年研发资金投入量![]() 和年销售额
和年销售额![]() 的数据,
的数据,![]() ,并对这些数据作了初步处理,得到了右侧的散点图及一些统计量的值.令
,并对这些数据作了初步处理,得到了右侧的散点图及一些统计量的值.令![]()
![]()
![]() ,经计算得如下数据:
,经计算得如下数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)设![]() 和
和![]() 的相关系数为
的相关系数为![]() ,
,![]() 和
和![]() 的相关系数为
的相关系数为![]() ,请从相关系数的角度,选择一个拟合程度更好的模型;
,请从相关系数的角度,选择一个拟合程度更好的模型;
(2)(i)根据(1的选择及表中数据,建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(ii)若下一年销售额![]() 需达到90亿元,预测下一年的研发资金投入量
需达到90亿元,预测下一年的研发资金投入量![]() 是多少亿元?
是多少亿元?
附:①相关系数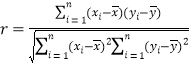 ,回归直线
,回归直线![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: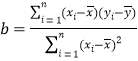 ,
,![]() ;
;
② 参考数据:![]() ,
,![]() ,
,![]() .
.
【答案】(1)模型![]() 的拟合程度更好;(2)(i)
的拟合程度更好;(2)(i)![]() ;(ii)
;(ii)![]() 亿元.
亿元.
【解析】
(1)由相关系数求出两个系数,比较大小可得;
(2)(i)先建立![]() 关于
关于![]() 的线性回归方程,从而得出
的线性回归方程,从而得出![]() 关于
关于![]() 的回归方程;
的回归方程;
(ii)把![]() 代入(i)中的回归方程可得
代入(i)中的回归方程可得![]() 值.
值.
本小题主要考查回归分析等基础知识,考查数据处理能力、运算求解能力、抽象概括能力及应用意识,考查统计与概率思想、分类与整合思想,考查数学抽象、数学运算、数学建模、数据分析等核心素养,体现基础性、综合性与应用性.
解:(1)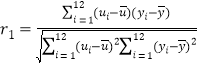
![]() ,
,
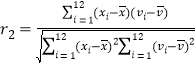
![]() ,
,
则![]() ,因此从相关系数的角度,模型
,因此从相关系数的角度,模型![]() 的拟合程度更好
的拟合程度更好
(2)(i)先建立![]() 关于
关于![]() 的线性回归方程.
的线性回归方程.
由![]() ,得
,得![]() ,即
,即![]() .
.
由于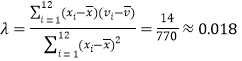 ,
,
![]()
所以![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,
,
所以![]() ,则
,则![]()
(ii)下一年销售额![]() 需达到90亿元,即
需达到90亿元,即![]() ,
,
代入![]() 得,
得,![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以预测下一年的研发资金投入量约是![]() 亿元
亿元


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点.
上一点.
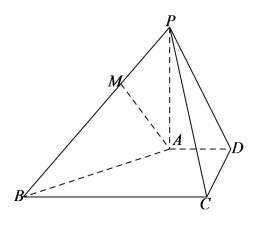
(I)若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(II)若![]() ,
,![]() ,异面直线
,异面直线![]() 与
与![]() 成
成![]() 角,二面角
角,二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长及直线
的长及直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】质检部门为了解某企业生产的一-种圆柱形零件的质量情况,随机抽检了100个零件,得到这些零件的横截面直径d(单位:![]() )的频率分布表如下:
)的频率分布表如下:
d的分组 |
|
|
|
|
|
零件数 | 12 | 38 | 38 | 10 | 2 |
(1)试估计这个企业生产的这类零件的横截面直径不低于![]() 的概率;
的概率;
(2)求这个企业生产的这类零件的横截面直径的平均数与标准差的估计值(同一组中的数据用该区间的中点值为代表).(精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某手机商城2018年华为、苹果、三星三种品牌的手机各季度销量的百分比堆积图(如:第三季度华为销量约占50%,苹果销量约占20%,三星销量约占30%).根据该图,以下结论中一定正确的是( )
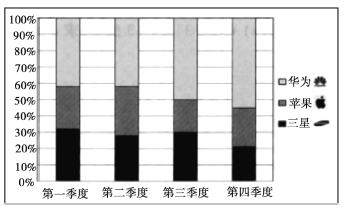
A.华为的全年销量最大B.苹果第二季度的销量大于第三季度的销量
C.华为销量最大的是第四季度D.三星销量最小的是第四季度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() 且右焦点
且右焦点![]() 到右准线
到右准线![]() 的距离为
的距离为![]() .
.
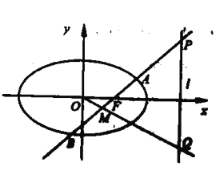
(1)求椭圆![]() 的标准方程:
的标准方程:
(2)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,与
两点,与![]() 交于点
交于点![]() 是弦
是弦![]() 的中点,直线
的中点,直线![]() 与
与![]() 交于点
交于点![]() .若
.若![]() 与
与![]() 的面积之比是
的面积之比是![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com