
【题目】已知直线![]() :
:![]() ,圆
,圆![]() :
:![]() .
.
(1)判断直线![]() 与圆的位置关系,并证明你的结论;
与圆的位置关系,并证明你的结论;
(2)直线![]() 过直线
过直线![]() 的定点且
的定点且![]() ,若
,若![]() 与圆
与圆![]() 交与
交与![]() 两点,
两点,![]() 与圆
与圆![]() 交与
交与![]() 两点,求
两点,求![]() 的最大值.
的最大值.
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆C的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,求证:
,求证:![]() 的面积为定值并求出定值
的面积为定值并求出定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列判断:①一条直线和一点确定一个平面;②两条直线确定一个平面;③三角形和梯形一定是平面图形;④三条互相平行的直线一定共面其中正确的是_______.(写出所有正确判断的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. ![]() ,
, ![]() 为不共线向量,若
为不共线向量,若![]() ,则
,则![]()
B. 若![]() ,
, ![]() 为平面内两个不相等向量,则平面内任意向量
为平面内两个不相等向量,则平面内任意向量![]() 都可以表示为
都可以表示为![]()
C. 若![]() ,
, ![]() ,则
,则![]() 与
与![]() 不一定共线
不一定共线
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一颗质地均匀的骰子先后抛掷2次,观察其向上的点数,分别记为![]() .
.
(1)若记“![]() ”为事件
”为事件![]() ,求事件
,求事件![]() 发生的概率;
发生的概率;
(2)若记“![]() ”为事件
”为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
⑴从区间![]() 内任取一个实数
内任取一个实数![]() ,设事件
,设事件![]() 表示“函数
表示“函数![]() 在区间
在区间![]() 上有两个不同的零点”,求事件
上有两个不同的零点”,求事件![]() 发生的概率;
发生的概率;
⑵若联系掷两次一颗均匀的骰子(骰子六个面上标注的点数分别为![]() )得到的点数分别为
)得到的点数分别为![]() 和
和![]() ,记事件
,记事件![]() 表示“
表示“![]() 在
在![]() 上恒成立”,求事件
上恒成立”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了一次“环保知识竞赛”活动. 为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为![]() )进行统计. 按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).
)进行统计. 按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).
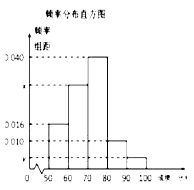

(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() ,
,![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动,设![]() 表示所抽取的3名同学中得分在[80,90)的学生人数,求
表示所抽取的3名同学中得分在[80,90)的学生人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com