
【题目】已知椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为椭圆
为椭圆![]() 上的三点,
上的三点,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,当
,当![]() 的中点恰为点
的中点恰为点![]() 时,判断
时,判断![]() 的面积是否为常数,并说明理由.
的面积是否为常数,并说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 的面积是常数为
的面积是常数为![]() ,理由见解析.
,理由见解析.
【解析】
(1)由题a=![]() 再由离心率,求得c,再由
再由离心率,求得c,再由![]() ,即可求得方程;(2)若点
,即可求得方程;(2)若点![]() 是椭圆的右顶点,求得
是椭圆的右顶点,求得![]() 的面积为
的面积为![]() ,若点
,若点![]() 不是椭圆的左、右顶点,则设直线
不是椭圆的左、右顶点,则设直线![]() 的方程为:
的方程为:![]() ,与椭圆联立,由韦达定理得
,与椭圆联立,由韦达定理得![]() 的坐标,弦长公式,点到线的距离公式,进而求出
的坐标,弦长公式,点到线的距离公式,进而求出![]() 的面积为常数
的面积为常数
(1)由已知易得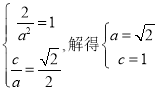 ,
,
∴![]() ,
,
故椭圆![]() 的标准方程为:
的标准方程为:![]() .
.
(2)①若点![]() 是椭圆的右顶点(左顶点一样),则
是椭圆的右顶点(左顶点一样),则![]() ,
,
∵![]() ,
,![]() 在线段
在线段![]() 上,
上,
∴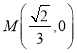 ,此时
,此时![]() 轴,求得
轴,求得![]() ,
,
∴![]() 的面积等于
的面积等于![]() .
.
②若点![]() 不是椭圆的左、右顶点,则设直线
不是椭圆的左、右顶点,则设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]() ,
,
由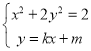 得
得![]() ,则
,则![]() ,
,![]() ,
,
∴![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,将其代入椭圆方程,化简得
,将其代入椭圆方程,化简得![]() .
.
∴![]()
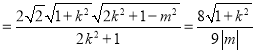 .
.
![]() 点
点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
∴![]() 的面积
的面积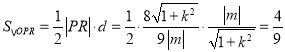 .
.
综上可知,![]() 的面积为常数
的面积为常数![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】环保部门要对所有的新车模型进行广泛测试,以确定它的行车里程的等级,下表是对100辆新车模型在一个耗油单位内行车里程(单位:公里)的测试结果.
分组 | 频数 |
| 6 |
| 10 |
| 20 |
| 30 |
| 18 |
| 12 |
| 4 |
(1)做出上述测试结果的频率分布直方图,并指出其中位数落在哪一组;
(2)用分层抽样的方法从行车里程在区间![]() 与
与![]() 的新车模型中任取5辆,并从这5辆中随机抽取2辆,求其中恰有一个新车模型行车里程在
的新车模型中任取5辆,并从这5辆中随机抽取2辆,求其中恰有一个新车模型行车里程在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老年人120人,中年人360人,青年人n人,为调查身体健康状况,需要从中抽取一个容量为m的样本,用分层抽样的方法进行抽样调查,样本中的中年人为6人,则n和m的值不可以是下列四个选项中的哪组( )
A.n=360,m=14B.n=420,m=15C.n=540,m=18D.n=660,m=19
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党中央、国务院历来高度重视青少年的健康成长.“少年强则国强”,青少年身心健康、体魄强健、意志坚强、充满活力,是一个民族旺盛生命力的体现,是社会文明进步的标志,是国家综合实力的重要方面.全面实施《国家学生体质健康标准》,把健康素质作为评价学生全面健康发展的重要指标,是新时代的要求.《国家学生体质健康标准》有一项指标是学生体质指数(![]() ),其计算公式为:
),其计算公式为: ,当
,当![]() 时,认为“超重”,应加强锻炼以改善
时,认为“超重”,应加强锻炼以改善![]() .某高中高一、高二年级学生共2000人,人数分布如表(a).为了解这2000名学生的
.某高中高一、高二年级学生共2000人,人数分布如表(a).为了解这2000名学生的![]() 指数情况,从中随机抽取容量为160的一个样本.
指数情况,从中随机抽取容量为160的一个样本.
表(a)
性别 年级 | 男生 | 女生 | 合计 |
高一年级 | 550 | 650 | 1200 |
高二年级 | 425 | 375 | 800 |
合计 | 975 | 1025 | 2000 |
(1)为了使抽取的160个学生更具代表性,宜采取分层抽样,试给出一个合理的分层抽样方案,并确定每层应抽取出的学生人数;
(2)分析这160个学生的![]() 值,统计出“超重”的学生人数分布如表(b).
值,统计出“超重”的学生人数分布如表(b).
表(b)
性别 年级 | 男生 | 女生 |
高一年级 | 4 | 6 |
高二年级 | 2 | 4 |
(ⅰ)试估计这2000名学生中“超重”的学生数;
(ⅱ)对于该校的2000名学生,应用独立性检验的知识,可分析出性别变量与年级变量哪一个与“是否超重”的关联性更强.应用卡方检验,可依次得到![]() 的观测值
的观测值![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 的大小关系.(只需写出结论)
的大小关系.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,
,![]() 是圆M内一定点,动点P为圆M上任意一点,线段PN的垂直平分线l和半径MP相交于点C.
是圆M内一定点,动点P为圆M上任意一点,线段PN的垂直平分线l和半径MP相交于点C.
(1)求点C的轨迹方程;
(2)设直线![]() 与C交于不同两点A,B,点O为坐标原点,当
与C交于不同两点A,B,点O为坐标原点,当![]() 的面积S取最大值时,求
的面积S取最大值时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方![]() 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价,现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价,现从评价系统中选出![]() 条较为详细的评价信息进行统计,车辆状况和优惠活动评价的
条较为详细的评价信息进行统计,车辆状况和优惠活动评价的![]() 列联表如下:
列联表如下:
对优惠活动好评 | 对优惠活动不满意 | 合计 | |
对车辆状况好评 |
|
|
|
对车辆状况不满意 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?
(2)为了回馈用户,公司通过![]() 向用户随机派送骑行券,用户可以将骑行券用于骑行付费,也可以通过
向用户随机派送骑行券,用户可以将骑行券用于骑行付费,也可以通过![]() 转赠给好友某用户共获得了
转赠给好友某用户共获得了![]() 张骑行券,其中只有
张骑行券,其中只有![]() 张是一元券现该用户从这张骑行券中随机选取
张是一元券现该用户从这张骑行券中随机选取![]() 张转赠给好友,求选取的
张转赠给好友,求选取的![]() 张中至少有
张中至少有![]() 张是一元券的概率.
张是一元券的概率.
附:下面的临界值表仅供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式: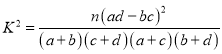 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学研究表明,人极易受情绪的影响,某选手参加7局4胜制的兵乒球比赛.
(1)在不受情绪的影响下,该选手每局获胜的概率为![]() ;但实际上,如果前一句获胜的话,此选手该局获胜的概率可提升到
;但实际上,如果前一句获胜的话,此选手该局获胜的概率可提升到![]() ;而如果前一局失利的话,此选手该局获胜的概率则降为
;而如果前一局失利的话,此选手该局获胜的概率则降为![]() ,求该选手在前3局获胜局数
,求该选手在前3局获胜局数![]() 的分布列及数学期望;
的分布列及数学期望;
(2)假设选手的三局比赛结果互不影响,且三局比赛获胜的概率为![]() ,记
,记![]() 为锐角
为锐角![]() 的内角,求证:
的内角,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且sin2A+sin2B+sin2C=sinAsinB+sinBsinC+sinCsin A.
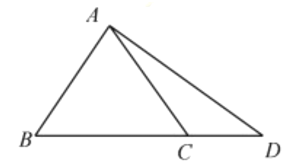
(1)证明:△ABC是正三角形;
(2)如图,点D在边BC的延长线上,且BC=2CD,AD![]() ,求sin∠BAD的值.
,求sin∠BAD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com