
【题目】已知向量![]() ,向量
,向量![]() ,且函数
,且函数![]() .
.
(1)求函数![]() 的单调递增区间及其对称中心;
的单调递增区间及其对称中心;
(2)在![]() 中,角A,B,C所对的边分别为a,b,c且角A满足
中,角A,B,C所对的边分别为a,b,c且角A满足![]() .若
.若![]() ,BC边上的中线长为3,求
,BC边上的中线长为3,求![]() 的面积S.
的面积S.
(3)将函数![]() 的图像向左平移
的图像向左平移![]() 个长度单位,向下平移
个长度单位,向下平移![]() 个长度单位,再横坐标不变,纵坐标缩短为原来的
个长度单位,再横坐标不变,纵坐标缩短为原来的![]() 后得到函数
后得到函数![]() 的图像,令函数
的图像,令函数![]() 在
在![]() 的最小值为
的最小值为![]() ,求正实数
,求正实数![]() 的值.
的值.
【答案】(1)单调递增区间:![]() ,对称中心
,对称中心![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据平面向量数量积的定义,结合诱导公式及正余弦二倍角公式化简即可得函数![]() 解析式.进而求得单调区间及对称中心.
解析式.进而求得单调区间及对称中心.
(2)将![]() 代入(1)中所得解析式,即可由
代入(1)中所得解析式,即可由![]() 求得
求得![]() .结合向量的加法与减法运算和BC边上的中线长,即可求得
.结合向量的加法与减法运算和BC边上的中线长,即可求得![]() .再根据三角形面积公式即可求解.
.再根据三角形面积公式即可求解.
(3)根据函数的平移变换,即可求得![]() 的解析式.代入后表示出
的解析式.代入后表示出![]() 的解析式.转化为关于
的解析式.转化为关于![]() 的二次函数性质,通过对
的二次函数性质,通过对![]() 分类讨论并结合最小值,即可求得
分类讨论并结合最小值,即可求得![]() 的值.
的值.
(1)因为![]() 代入向量
代入向量![]() ,向量
,向量![]() ,结合诱导公式及正余弦的二倍角公式化简可得
,结合诱导公式及正余弦的二倍角公式化简可得
![]()
所以![]()
![]()
![]()
函数![]() 的单调递增区间满足
的单调递增区间满足![]()
解得![]()
所以函数![]() 的单调递增区间为
的单调递增区间为![]()
令![]() ,解得
,解得![]()
则对称中心![]()
(2)![]() ,得
,得![]() ,
,
则![]() ,
,
∴![]()
又![]() ①,
①,
BC上的中线长为3,则![]() ②
②
由①②知:![]()
即![]() ,所以
,所以![]()
∴![]()
(3)由题意将函数![]() 的图像向左平移
的图像向左平移![]() 个长度单位可得
个长度单位可得![]()
向下平移![]() 个长度单位,可得
个长度单位,可得![]()
再横坐标不变,纵坐标缩短为原来的![]() 后得到函数
后得到函数![]() ,则
,则![]()
则![]() ,
,
所以![]() ,
,![]() ,
,
①当![]() 时,当
时,当![]() 时,
时,![]() 有最小值
有最小值![]() ,解得
,解得![]() .
.
②当![]() 时,当
时,当![]() 时,
时,![]() 有最小值
有最小值![]() ,
,
![]() (舍去),
(舍去),
综上可得![]() .
.


科目:高中数学 来源: 题型:
【题目】给出下列命题,其中所有正确命题的序号是__________.
①抛物线![]() 的准线方程为
的准线方程为![]() ;
;
②过点![]() 作与抛物线
作与抛物线![]() 只有一个公共点的直线
只有一个公共点的直线![]() 仅有1条;
仅有1条;
③![]() 是抛物线
是抛物线![]() 上一动点,以
上一动点,以![]() 为圆心作与抛物线准线相切的圆,则此圆一定过定点
为圆心作与抛物线准线相切的圆,则此圆一定过定点![]() .
.
④抛物线![]() 上到直线
上到直线![]() 距离最短的点的坐标为
距离最短的点的坐标为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对数函数![]() (
(![]() 且
且![]() )和指数函数
)和指数函数![]() (
(![]() 且
且![]() )互为反函数.已知函数
)互为反函数.已知函数![]() ,其反函数为
,其反函数为![]() .
.
(1)若函数![]() 定义域为
定义域为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
(2)若![]() 为定义在
为定义在![]() 上的奇函数,且
上的奇函数,且![]() 时,
时,![]() .求
.求![]() 的解析式.
的解析式.
(3)定义在![]() 上的函数
上的函数![]() ,如果满足:对任意的
,如果满足:对任意的![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称函数
成立,则称函数![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 为函数
为函数![]() 的上界.若函数
的上界.若函数 ,当
,当![]() 时,探究函数
时,探究函数![]() 在
在![]() 上是否存在上界
上是否存在上界![]() ,若存在求出
,若存在求出![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f (x) = x ex (xR)
(Ⅰ)求函数 f (x)的单调区间和极值;
(Ⅱ)若x (0, 1), 求证: f (2 x) > f (x);
(Ⅲ)若x1 (0, 1), x2(1, +∞), 且 f (x1) = f (x2), 求证: x1 + x2 > 2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60][60,70][70,80][80,90][90,100].

(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业节能降耗技术改造后,在生产某产品过程中的产量x(吨)与相应的生产能耗y(吨)的几组对应数据如表所示:
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
若根据表中数据得出y关于x的线性回归方程为![]() 0.7x+a,若生产7吨产品,预计相应的生产能耗为( )吨.
0.7x+a,若生产7吨产品,预计相应的生产能耗为( )吨.
A.5.25B.5.15C.5.5D.9.5
查看答案和解析>>
科目:高中数学 来源: 题型:
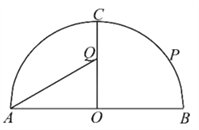
【题目】如图,某景区内有一半圆形花圃,其直径![]() 为
为![]() ,
,![]() 是圆心,且
是圆心,且![]() .在
.在![]() 上有一座观赏亭
上有一座观赏亭![]() ,其中
,其中![]() .计划在
.计划在![]() 上再建一座观赏亭
上再建一座观赏亭![]() ,记
,记![]() .
.
(1)当![]() 时,求
时,求![]() 的大小;
的大小;
(2)当![]() 越大,游客在观赏亭
越大,游客在观赏亭![]() 处的观赏效果越佳,求游客在观赏亭
处的观赏效果越佳,求游客在观赏亭![]() 处的观赏效果最佳时,角
处的观赏效果最佳时,角![]() 的正弦值.
的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com