
【题目】某市为了鼓励市民节约用水,实行“阶梯式”水价,将该市每户居民的月用水量划分为三档:月用水量不超过4吨的部分按2元/吨收费,超过4吨但不超过8吨的部分按4元/吨收费,超过8吨的部分按8元/吨收费.
(1)求居民月用水量费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:吨)的函数解析式;
(单位:吨)的函数解析式;
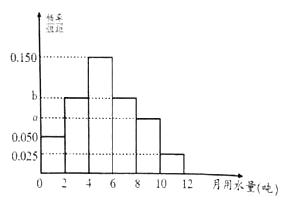
(2)为了了解居民的用水情况,通过抽样,获得今年3月份100户居民每户的用水量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年3月份用水费用不超过16元的占60%,求![]() 的值;
的值;
(3)若地区居民用水量平均值超过6吨,则说明该地区居民用水没有节约意识在满足(2)的条件下,请你估计![]() 市居民用水是否有节约意识(同一组中的数据用该组区间的中点值作代表).
市居民用水是否有节约意识(同一组中的数据用该组区间的中点值作代表).
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且A,B,C成等差数列
(1)若b=2 ![]() ,c=2,求△ABC的面积;
,c=2,求△ABC的面积;
(2)若a,b,c成等比数列,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用水,实行“阶梯式”水价,将该市每户居民的月用水量划分为三档:月用水量不超过4吨的部分按2元/吨收费,超过4吨但不超过8吨的部分按4元/吨收费,超过8吨的部分按8元/吨收费.
(1)求居民月用水量费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:吨)的函数解析式;
(单位:吨)的函数解析式;
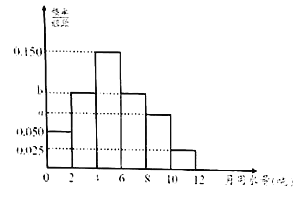
(2)为了了解居民的用水情况,通过抽样,获得今年3月份100户居民每户的用水量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年3月份用水费用不超过16元的占66%,求![]() 的值;
的值;
(3)在满足条件(2)的条件下,若以这100户居民用水量的频率代替该月全市居民用户用水量的概率.且同组中的数据用该组区间的中点值代替.记为该市居民用户3月份的用水费用,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的各项均为正数,且a1a100+a3a98=8,则log2a1+log2a2+…+log2a100=( )
A.10
B.50
C.100
D.1000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解2013年某校高三学生的视力情况,随机抽查了一部分学生视力,将调查结果分组,分组区间为![]() ,
,![]() ,… ,
,… ,![]() 经过数据处理,得到如右频率分布表:
经过数据处理,得到如右频率分布表:
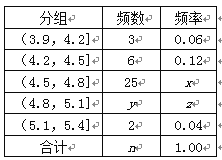
(1)求频率分布表中未知量![]() 的值;
的值;
(2)从样本中视力在![]() 和
和![]() 的所有同学中随机抽取两人,求两人的视力差的绝对值低于0.5的概率.
的所有同学中随机抽取两人,求两人的视力差的绝对值低于0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从![]() 个招标问题中随机抽取
个招标问题中随机抽取![]() 个问题,已知这
个问题,已知这![]() 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的![]() 道題目,而乙公司能正确回答毎道题目的概率均为
道題目,而乙公司能正确回答毎道题目的概率均为![]() ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲、乙两家公司共答对![]() 道题目的概率;
道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com