
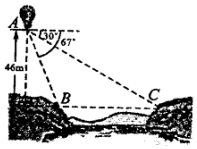
 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于60m.(用四舍五入法将结果精确到个位.参考数据:sin67°≈0.92,cos67°≈0.39,sin37°≈0.60,cos37°≈0.80,$\sqrt{3}$≈1.73.
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于60m.(用四舍五入法将结果精确到个位.参考数据:sin67°≈0.92,cos67°≈0.39,sin37°≈0.60,cos37°≈0.80,$\sqrt{3}$≈1.73. 分析 过A点作AD垂直于CB的延长线,垂足为D,分别在Rt△ACD、Rt△ABD中利用三角函数的定义,算出CD、BD的长,从而可得BC,即为河流在B、C两地的宽度.
解答 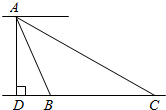 解:过A点作AD垂直于CB的延长线,垂足为D,
解:过A点作AD垂直于CB的延长线,垂足为D,
则Rt△ACD中,∠C=30°,AD=46m,
AB=$\frac{46}{sin67°}$,
根据正弦定理
得BC=$\frac{ABsin37°}{sin30°}$=$46×\frac{sin37°}{sin67°sin30°}$≈60m.
故答案为:60.
点评 本题给出实际应用问题,求河流在B、C两地的宽度,着重考查了三角函数的定义、正余弦定理解三角形的知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x | B. | y=${log}_{\frac{1}{2}}$x | C. | y=x-1 | D. | y=x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y全不为0,则x2+y2≠0” | |
| B. | 若命题$p:?{x_0}∈R,{x_0}^2-{x_0}+1<0$,则?p:?x∉R,x2-x+1≥0 | |
| C. | 若命题“p或q”为真命题,则命题p和命题q均为真命题 | |
| D. | “x>3”是“x>2”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1]∪[3,+∞) | B. | [1,3] | C. | $[{\frac{3}{2},3}]$ | D. | $({-∞,\frac{3}{2}}]∪[{3,+∞})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com