
【题目】如图,在直三棱柱ABCA1B1C1中,∠ABC=![]() ,D是棱AC的中点,且AB=BC=BB1=2.
,D是棱AC的中点,且AB=BC=BB1=2.
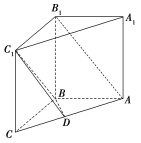
(1)求证:AB1∥平面BC1D;
(2)求异面直线AB1与BC1的夹角.
 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】对于集合![]() ,定义函数
,定义函数![]() 对于两个集合
对于两个集合![]() ,定义集合
,定义集合![]() . 已知
. 已知![]() ,
, ![]() .
.
(Ⅰ)写出![]() 和
和![]() 的值,并用列举法写出集合
的值,并用列举法写出集合![]() ;
;
(Ⅱ)用![]() 表示有限集合
表示有限集合![]() 所含元素的个数,求
所含元素的个数,求![]() 的最小值;
的最小值;
(Ⅲ)有多少个集合对![]() ,满足
,满足![]() ,且
,且![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:函数f(x)=lg(ax2-x+16a)的定义域为R;命题q:不等式3x-9x<a对任意x∈R恒成立.
(1)如果p是真命题,求实数a的取值范围;
(2)如果命题“p或q”为真命题且“p且q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
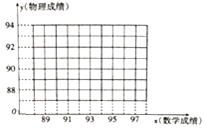
【题目】一次考试中,5名同学的数学、物理成绩如表所示:
学生 |
|
|
|
|
|
数学 | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
![]() 请在图中的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
请在图中的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
![]() 要从4名数学成绩在90分以上的同学中选2名参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望
要从4名数学成绩在90分以上的同学中选2名参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望![]() .
.
参考公式:线性回归方程![]() ;,其中
;,其中![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,其长轴、焦距和短轴的长的平方依次成等差数列
,其长轴、焦距和短轴的长的平方依次成等差数列![]() 直线l与x轴正半轴和y轴分别交于点Q、P,与椭圆分别交于点M、N,各点均不重合且满足
直线l与x轴正半轴和y轴分别交于点Q、P,与椭圆分别交于点M、N,各点均不重合且满足![]() .
.
![]() 求椭圆的标准方程;
求椭圆的标准方程;
![]() 若
若![]() ,试证明:直线l过定点并求此定点.
,试证明:直线l过定点并求此定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com