
【题目】已知二次函数f(x)=ax2+bx+c.
(1)若a=c>0,f(1)=1,对任意x∈|[﹣2,2],f(x)的最大值与最小值之和为g(a),求g(a)的表达式;
(2)若a,b,c为正整数,函数f(x)在(﹣ ![]() ,
, ![]() )上有两个不同零点,求a+b+c的最小值.
)上有两个不同零点,求a+b+c的最小值.
【答案】
(1)解:a=c>0,f(1)=1,则a+b+a=1,b=1﹣2a,
∴f(x))=ax2+(1﹣2a)x+a=a ![]() +
+ ![]() ,
,
当1﹣ ![]() ≤﹣2,即0<a≤
≤﹣2,即0<a≤ ![]() 时,g(a)=f(﹣2)+f(2)=10a;
时,g(a)=f(﹣2)+f(2)=10a;
当﹣2<1﹣ ![]() ≤0,即
≤0,即 ![]() <a≤
<a≤ ![]() 时,g(a)=f(1﹣
时,g(a)=f(1﹣ ![]() )+f(2)=a﹣
)+f(2)=a﹣ ![]() +3,
+3,
当a> ![]() 时,g(a)=f(1﹣
时,g(a)=f(1﹣ ![]() )+f(﹣2)=9a﹣
)+f(﹣2)=9a﹣ ![]() ﹣1,
﹣1,
综上所述,g(a)= 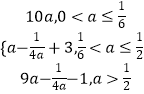
(2)解:函数f(x)在(﹣ ![]() ,
, ![]() )上有两个不同零点x1,x2,则x1+x2=﹣
)上有两个不同零点x1,x2,则x1+x2=﹣ ![]() <0,
<0, ![]() >x1x2=
>x1x2= ![]() >0
>0
∴a>16c,
由根的分布可知f(﹣ ![]() )=
)= ![]() a﹣
a﹣ ![]() b+c>0,即a+16c>4b,
b+c>0,即a+16c>4b,
∵a,b,c为正整数,∴a+16c≥4b+1
f(0)=c>0,△>0,b ![]() ,
,
∴a+16c>8 ![]() +1,可得(
+1,可得( ![]() )2>1,
)2>1,
∵a>16c,∴ ![]() >1,
>1,
∴ ![]() ,∴a>25,
,∴a>25,
∴a≥26,
∴b ![]() ≥
≥ ![]() ,∴b≥11,c≥1.
,∴b≥11,c≥1.
f(x)=26x2+11x+1,经检验符合题意,故a+b+c的最小值为38
【解析】(1)配方,分类讨论,求g(a)的表达式;(2)若a,b,c为正整数,函数f(x)在(﹣ ![]() ,
, ![]() )上有两个不同零点,确定a,b,c的范围,即可求a+b+c的最小值.
)上有两个不同零点,确定a,b,c的范围,即可求a+b+c的最小值.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+
,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+ ![]() 的取值范围是( )
的取值范围是( )
A.(﹣1,+∞)
B.(﹣1,1]
C.(﹣∞,1)
D.[﹣1,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系如图一的一条折线表示;西红柿的种植成本与上市时间的关系如图二的抛物线段表示. 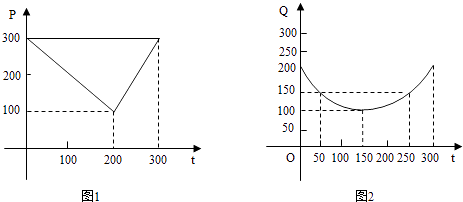
(1)写出图一表示的市场售价与时间的函数关系式p=f(t);写出图二表示的种植成本与时间的函数关系式Q=g(t);
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价各种植成本的单位:元/102㎏,时间单位:天)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x﹣ ![]() )+
)+ ![]() .
.
(1)求函数f(x)的对称轴方程;
(2)若方程sin2x+2|f(x+ ![]() )|﹣m+1=0在x∈[﹣
)|﹣m+1=0在x∈[﹣ ![]() ,
, ![]() ]上有三个实数解,求实数m的取值范围.
]上有三个实数解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,A(a,0),B(0,b),O(0,0),△OAB的面积为4,
,A(a,0),B(0,b),O(0,0),△OAB的面积为4,
(1)求椭圆的标准方程
(2)设直线l:y=kx+1与椭圆C相交于P,Q两点,是否存在这样的实数k,使得以PQ为直径的圆过原点,若存在,请求出k的值:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中正确的有
①函数y= ![]() 的定义域是{x|x≠0};
的定义域是{x|x≠0};
②lg ![]() =lg(x﹣2)的解集为{3};
=lg(x﹣2)的解集为{3};
②31﹣x﹣2=0的解集为{x|x=1﹣log32};
④lg(x﹣1)<1的解集是{x|x<11}.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com