
【题目】已知函数![]() .
.
(1)若![]() ,证明:
,证明:![]() ;
;
(2)若![]() 只有一个极值点,求
只有一个极值点,求![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)将![]() 代入
代入![]() ,可得
,可得![]() 等价于
等价于![]() ,即
,即![]() ,令
,令![]() ,求出
,求出![]() ,可得
,可得![]() 的最小值,可得证;
的最小值,可得证;
(2)分![]() ,
,![]() 三种情况讨论,分别对
三种情况讨论,分别对![]() 求导,其中
求导,其中![]() 又分①若
又分①若![]() ②
②![]() ③
③![]() 三种情况,利用函数的零点存在定理可得a的取值范围.
三种情况,利用函数的零点存在定理可得a的取值范围.
解:(1)当![]() 时,
时,![]() 等价于
等价于![]() ,即
,即![]() ;
;
设函数![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增.
单调递增.
故![]() 为
为![]() 的最小值,
的最小值,
而![]() ,故
,故![]() ,即
,即![]() .
.
(2)![]() ,
,
设函数![]()
![]() ,则
,则![]() ;
;
(i)当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,取b满足
,取b满足![]() 且
且![]() ,则
,则![]() ,
,
故![]() 在
在![]() 上有唯一一个零点
上有唯一一个零点![]() ,
,
且当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
由于![]() ,所以
,所以![]() 是
是![]() 的唯一极值点;
的唯一极值点;
(ii)当![]() 时,
时,![]() 在
在![]() 上单调递增,无极值点;
上单调递增,无极值点;
(iii)当![]() 时,若
时,若![]() 时,
时,![]() ;若
;若![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增.
单调递增.
故![]() 为
为![]() 的最小值,
的最小值,
①若![]() 时,由于
时,由于![]() ,故
,故![]() 只有一个零点,所以
只有一个零点,所以![]() 时
时![]() ,
,
因此![]() 在
在![]() 上单调递增,故
上单调递增,故![]() 不存在极值;
不存在极值;
②若![]() 时,由于
时,由于![]() ,即
,即![]() ,所以
,所以![]() ,
,
因此![]() 在
在![]() 上单调递增,故
上单调递增,故![]() 不存在极值;
不存在极值;
③若![]() 时,
时,![]() ,即
,即![]() .
.
又![]() ,且
,且![]() ,
,
而由(1)知![]() ,所以
,所以![]() ,
,
取c满足![]() ,则
,则![]()
故![]() 在
在![]() 有唯一一个零点
有唯一一个零点![]() ,在
,在![]() 有唯一一个零点
有唯一一个零点![]() ;
;
且当![]() 时
时![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
由于![]() ,故
,故![]() 在
在![]() 处取得极小值,在
处取得极小值,在![]() 处取得极大值,
处取得极大值,
即![]() 在
在![]() 上有两个极值点.
上有两个极值点.
综上,![]() 只有一个极值点时,
只有一个极值点时,![]() 的取值范围是
的取值范围是![]()


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】某单位从一所学校招收某类特殊人才.对![]() 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
| 一般 | 良好 | 优秀 |
一般 |
|
|
|
良好 |
|
|
|
优秀 |
|
|
|
例如表中运动协调能力良好且逻辑思维能力一般的学生是![]() 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这![]() 位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)从运动协调能力为优秀的学生中任意抽取![]() 位,求其中至少有一位逻辑思维能力优秀的学生的概率.
位,求其中至少有一位逻辑思维能力优秀的学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设四边形![]() 为矩形,点
为矩形,点![]() 为平面
为平面![]() 外一点,且
外一点,且![]() 平面
平面![]() ,若
,若![]() ,
,![]() .
.
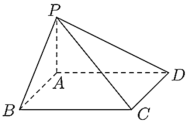
(1)求![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(2)在![]() 边上是否存在一点
边上是否存在一点![]() ,使得点
,使得点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)若点![]() 是
是![]() 的中点,在
的中点,在![]() 内确定一点
内确定一点![]() ,使
,使![]() 的值最小,并求此时
的值最小,并求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年,国际权威机构IDC发布的全球手机销售报告显示:华为突破2亿台出货量超越苹果的出货量,首次成为全球第二,华为无愧于中国最强的高科技企业。华为业务CEO余承东明确表示,华为的目标,就是在2021年前,成为全球最大的手机厂商.为了解华为手机和苹果手机使用的情况是否和消费者的性别有关,对100名华为手机使用者和苹果手机使用者进行统计,统计结果如下表:
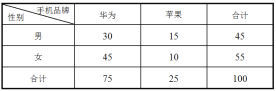
根据表格判断是否有95%的把握认为使用哪种品牌手机与性别有关系,则下列结论正确的是( )
附:![]()
![]()
A. 没有95%把握认为使用哪款手机与性别有关
B. 有95%把握认为使用哪款手机与性别有关
C. 有95%把握认为使用哪款手机与性别无关
D. 以上都不对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两焦点在
的两焦点在![]() 轴上,且短轴的两个顶点与其中一个焦点的连线构成斜边为
轴上,且短轴的两个顶点与其中一个焦点的连线构成斜边为![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求椭圆的方程;
(2)动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点![]() ,使得以线段
,使得以线段![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年数学竞赛请自以为来自X星球的选手参加填空题比赛,共10道题目,这位选手做题有一个古怪的习惯:先从最后一题(第10题)开始往前看,凡是遇到会的题就作答,遇到不会的题目先跳过(允许跳过所有的题目),一直看到第1题;然后从第1题开始往后看,凡是遇到先前未答的题目就随便写个答案,遇到先前已答的题目则跳过(例如,他可以按照9,8,7,4,3,2,1,5,6,10的次序答题),这样所有的题目均有作答,设这位选手可能的答题次序有n种,则n的值为( )
A.512B.511C.1024D.1023
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com