
【题目】已知曲线C1在平面直角坐标系中的参数方程为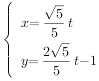 (t为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,有曲线C2:ρ=2cosθ-4sinθ
(t为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,有曲线C2:ρ=2cosθ-4sinθ
(1)将C1的方程化为普通方程,并求出C2的平面直角坐标方程
(2)求曲线C1和C2两交点之间的距离.
【答案】(1) y=2x-1, x2+y2=2x-4y (2) ![]()
【解析】试题分析:(1)曲线C1在平面直角坐标系中的参数方程为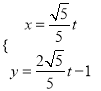 (t为参数),消去参数t可得普通方程.由曲线C2:ρ=2cosθ-4sinθ,即ρ2=ρ(2cosθ-4sinθ),利用互化公式可得直角坐标方程.
(t为参数),消去参数t可得普通方程.由曲线C2:ρ=2cosθ-4sinθ,即ρ2=ρ(2cosθ-4sinθ),利用互化公式可得直角坐标方程.
(2)x2+y2=2x-4y.化为(x-1)2+(y+2)2=5.可得圆心C2(1,-2),半径r=![]() .求出圆心到直线的距离d,可得曲线C1和C2两交点之间的距离=2
.求出圆心到直线的距离d,可得曲线C1和C2两交点之间的距离=2![]() .
.
试题解析:
(1)曲线C1在平面直角坐标系中的参数方程为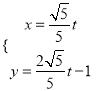 (t为参数),消去参数t可得普通方程:y=2x-1.
(t为参数),消去参数t可得普通方程:y=2x-1.
由曲线C2:ρ=2cosθ-4sinθ,即ρ2=ρ(2cosθ-4sinθ),可得直角坐标方程:x2+y2=2x-4y.
(2)x2+y2=2x-4y.化为(x-1)2+(y+2)2=5.可得圆心C2(1,-2),半径r=![]() .
.
∴曲线C1和C2两交点之间的距离=2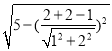 =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】已知点(1, ![]() )是函数f(x)=
)是函数f(x)= ![]() ax(a>0,a≠1)图象上一点,等比数列{an}的前n项和为c﹣f(n).数列{bn}(bn>0)的首项为2c,前n项和满足
ax(a>0,a≠1)图象上一点,等比数列{an}的前n项和为c﹣f(n).数列{bn}(bn>0)的首项为2c,前n项和满足 ![]() =
= ![]() +1(n≥2). (Ⅰ)求数列{an}的通项公式;
+1(n≥2). (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{ ![]() }的前n项和为Tn , 问使Tn>
}的前n项和为Tn , 问使Tn> ![]() 的最小正整数n是多少?
的最小正整数n是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,g(x)=f(x)﹣a
,g(x)=f(x)﹣a
(1)当a=2时,求函数g(x)的零点;
(2)若函数g(x)有四个零点,求a的取值范围;
(3)在(2)的条件下,记g(x)得四个零点分别为x1 , x2 , x3 , x4 , 求x1+x2+x3+x4的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f1(x),f2(x),h(x),如果存在实数a,b使得h(x)=af1(x)+bf2(x),那么称h(x)为f1(x),f2(x)的生成函数.
(1)给出函数 ![]() ,h(x)是否为f1(x), f2(x)的生成函数?并说明理由;
,h(x)是否为f1(x), f2(x)的生成函数?并说明理由;
(2)设 ![]() ,生成函数h(x).若不等式3h2(x)+2h(x)+t>0在x∈[2,4]上恒成立,求实数t的取值范围;
,生成函数h(x).若不等式3h2(x)+2h(x)+t>0在x∈[2,4]上恒成立,求实数t的取值范围;
(3)设 ![]() ,取a>0,b>0,生成函数h(x)图象的最低点坐标为(2,8).若对于任意正实数x1 , x2且x1+x2=1.试问是否存在最大的常数m,使h(x1)h(x2)≥m恒成立?如果存在,求出这个m的值;如果不存在,请说明理由.
,取a>0,b>0,生成函数h(x)图象的最低点坐标为(2,8).若对于任意正实数x1 , x2且x1+x2=1.试问是否存在最大的常数m,使h(x1)h(x2)≥m恒成立?如果存在,求出这个m的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于实数a和b,定义运算“*”: ![]() ,设f(x)=(2x﹣1)*(x﹣1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1 , x2 , x3 , 则实数m的取值范围是;x1+x2+x3的取值范围是 .
,设f(x)=(2x﹣1)*(x﹣1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1 , x2 , x3 , 则实数m的取值范围是;x1+x2+x3的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆(MN和AB、DC不重合). 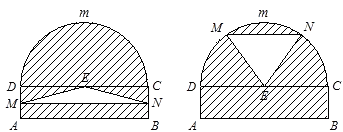
(1)当MN和AB之间的距离为1米时,求此时三角通风窗EMN的通风面积;
(2)设MN与AB之间的距离为x米,试将三角通风窗EMN的通风面积S(平方米)表示成关于x的函数S=f(x);
(3)当MN与AB之间的距离为多少米时,三角通风窗EMN的通风面积最大?并求出这个最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=(﹣x2+ax)ex , (x∈R,e为自然对数的底数)
(1)当a=2时,求函数f(x)的单调递增区间.
(2)函数f(x)是否为R上的单调函数,若是,求出a的取值范围;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:在四棱锥V﹣ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为 ![]() 的等腰三角形.
的等腰三角形. 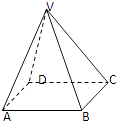
(1)求二面角V﹣AB﹣C的平面角的大小;
(2)求四棱锥V﹣ABCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com