
【题目】如图,PA垂直于以AB为直径的圆所在平面,C为圆上异于A,B的任意一点,![]() 垂足为E,点F是PB上一点,则下列判断中不正确的是( )﹒
垂足为E,点F是PB上一点,则下列判断中不正确的是( )﹒
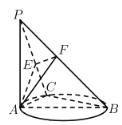
A.![]() 平面PACB.
平面PACB.![]() C.
C.![]() D.平面
D.平面![]() 平面PBC
平面PBC
 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】扎比瓦卡是2018年俄罗斯世界杯足球赛吉祥物,该吉祥物以西伯利亚平原狼为蓝本.扎比瓦卡,俄语意为“进球者”.某厂生产“扎比瓦卡”的固定成本为15000元,每生产一件“扎比瓦卡”需要增加投入20元,根据初步测算,每个销售价格满足函数 ,其中x是“扎比瓦卡”的月产量(每月全部售完).
,其中x是“扎比瓦卡”的月产量(每月全部售完).
(1)将利润![]() 表示为月产量
表示为月产量![]() 的函数;
的函数;
(2)当月产量为何值时,该厂所获利润最大?最大利润是多少?(总收益=总成本+利润).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是各项均为正数的等比数列,且b1=a1=1,b3=a4,b1+b2+b3=a3+a4.
(1)求数列{an},{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() :
: ![]() 的焦点,点
的焦点,点![]() 是准线
是准线![]() 上的动点,直线
上的动点,直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,若点
两点,若点![]() 的纵坐标为
的纵坐标为![]() ,点
,点![]() 为准线
为准线![]() 与
与![]() 轴的交点.
轴的交点.
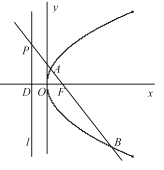
(1)求直线![]() 的方程;
的方程;
(2)求![]() 的面积
的面积![]() 范围.
范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 左右焦点为
左右焦点为![]() ,左顶点为A(-2.0),上顶点为B,且∠
,左顶点为A(-2.0),上顶点为B,且∠![]() =
=![]() .
.
(1)求椭圆C的方程;
(2)探究![]() 轴上是否存在一定点P,过点P的任意直线与椭圆交于M、N不同的两点,M、N不与点A重合,使得
轴上是否存在一定点P,过点P的任意直线与椭圆交于M、N不同的两点,M、N不与点A重合,使得 ![]() 为定值,若存在,求出点P;若不存在,说明理由.
为定值,若存在,求出点P;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com