
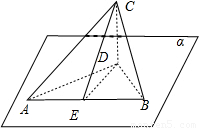
 解:过点C做CD垂直平面α,CE垂直AB,连接AD,BD,CE,DE
解:过点C做CD垂直平面α,CE垂直AB,连接AD,BD,CE,DE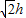 ,
,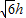
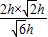 =
=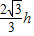 ,
,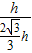 =
=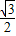 .
.

科目:高中数学 来源:黄冈重点作业·高二数学(下) 题型:013
Rt△ABC的斜边在平面α内,顶点A在α外,∠BAC在平面内的射影是∠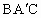 ,则∠
,则∠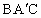 的范围为
的范围为
[ ]
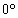 ,
,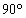 )
)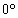 ,
,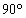 ]
]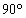 ,
,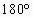 )
)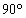 ,
,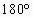 ]
]查看答案和解析>>
科目:高中数学 来源: 题型:
A.一条线段
B.一个锐角三角形
C.一个钝角三角形
D.一条线段或一个钝角三角形
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省天水一中高一(上)期末数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com