
【题目】已知![]() 为抛物线
为抛物线![]() 的焦点,过点
的焦点,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,抛物线
,抛物线![]() 在
在![]() 两点处的切线分别是
两点处的切线分别是![]() ,且
,且![]() 相交于点
相交于点![]() .设
.设![]() ,则
,则![]() 的值是___(结果用
的值是___(结果用![]() 表示).
表示).
【答案】![]()
【解析】
设A(x1,y1),B(x1,y2),设AB:y=kx+1,代入抛物线方程,消去y得,根据韦达定理可得x1+x2=4k,x1x2=﹣4,根据|AB|=y1+y2+2=m,可得4k2+4=m,根据导数的几何意义可得切线方程,求出点P的坐标,即可求出|PF|的值.
设A(x1,y1),B(x1,y2),
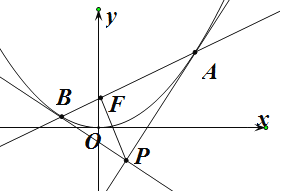
设AB:y=kx+1,代入抛物线方程,消去y得,x2﹣4kx﹣4=0,
则x1+x2=4k,x1x2=﹣4,
∴y1+y2=k(x1+x2)+2=4k2+2,
∵|AB|=y1+y2+2=m,
∴4k2+4=m
由抛物线C:x2=4y可得y![]() x2两边对x求导数,得到y′
x2两边对x求导数,得到y′![]() x,则切线l1的斜率为
x,则切线l1的斜率为![]() x1,切线l2的斜率为
x1,切线l2的斜率为![]() x2,
x2,
∴直线l1的方程为y﹣y1![]() x1(x﹣x1),即y
x1(x﹣x1),即y![]() x1x
x1x![]() x12,①
x12,①
则直线l2的方程为y﹣y2![]() x2(x﹣x2),即y
x2(x﹣x2),即y![]() x2x
x2x![]() x22,②,
x22,②,
由①②解得x![]() 2k,y
2k,y![]() 1,
1,
∴点P的坐标为(2k,﹣1),
根据两点间距离公式得到:|PF|![]() ,
,
故答案为:![]() .
.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】据《人民网》报道,“美国国家航空航天局( NASA)发文称,相比20年前世界变得更绿色了,卫星资料显示中国和印度的行动主导了地球变绿.”据统计,中国新增绿化面积的420/0来自于植树造林,下表是中国十个地区在2017年植树造林的相关数据.(造林总面积为人工造林、飞播造林、新封山育林、退化林修复、人工更新的面积之和)
单位:公顷
按造林方式分 | ||||||
地区 | 造林总面积 | 人工造林 | 飞播造林 | 新封山育林 | 退化林修复 | 人工更新 |
内蒙 | 618484 | 311052 | 74094 | 136006 | 90382 | 6950 |
河北 | 583361 | 345625 | 33333 | 135107 | 65653 | 3643 |
河南 | 149002 | 97647 | 13429 | 221117 | 15376 | 133 |
重庆 | 226333 | 100600 | 、 62400 | 63333 | ||
陕西 | 297642 | 184108 | 33602 | 63865 | 16067 | |
甘肃 | 325580 | 260144 | 57438 | 7998 | ||
新疆 | 263903 | 118105 | 6264 | 126647 | 10796 | 2091 |
青海 | 178414 | 16051 | 159734 | 2629 | ||
宁夏 | 91531 | 58960 | 22938 | 8298 | 1335 | |
北京 | 19064 | 10012、 | 4000 | 3999 | 1053 | |
(1)请根据上述数据,分别写出在这十个地区中人工造林面积与造林总面积的比值最大和最小的地区;
(2)在这十个地区中,任选一个地区,求该地区人工造林面积与造林总面积的比值不足50%的概率是多少?
(3)从上表新封山育林面积超过十万公顷的地区中,任选两个地区,求至少有一个地区退化林修复面积超过五万公顷的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某些竞赛活动中,选手的最终成绩是将前面所有轮次比赛成绩求算术平均获得的.同学们知道这样一个事实:在所有轮次的成绩中,如果由高到低依次去掉一些高分,那么平均分降低;反之,如果由低到高依次去掉一些低分,那么平均分提高. 这两个事实可以用数学语言描述为:若有限数列![]() 满足
满足![]() ,且
,且![]() 不全相等,则(1)_______;(2)_______.
不全相等,则(1)_______;(2)_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“有黑扫黑、无黑除恶、无恶治乱”,维护社会稳定和和平发展.扫黑除恶期间,大量违法分子主动投案,某市公安机关对某月连续7天主动投案的人员进行了统计,![]() 表示第
表示第![]() 天主动投案的人数,得到统计表格如下:
天主动投案的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 5 | 5 | 6 | 7 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判定变量![]() 与
与![]() 之间是正相关还是负相关.(写出正确答案,不用说明理由)
之间是正相关还是负相关.(写出正确答案,不用说明理由)
(3)预测第八天的主动投案的人数(按四舍五入取到整数).
参考公式: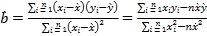 ,
, ![]() ./span>
./span>
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的一个焦点为
的一个焦点为![]() ,点
,点![]() 在
在![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,问
两点,问![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,求点
为直角顶点的等腰直角三角形?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面.有下列四个命题:
是三个不同的平面.有下列四个命题:
①若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() ,则
,则![]() ;
;
③若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
④若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
其中正确命题的序号是( )
A.①③B.①④C.②③④D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,其上一点
,其上一点![]() 在准线上的射影为
在准线上的射影为![]() ,△
,△![]() 恰为一个边长为4的等边三角形.
恰为一个边长为4的等边三角形.
(1)求抛物线![]() 的方程;
的方程;
(2)若过定点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为坐标原点)的面积为
为坐标原点)的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com