已知
2x2+2x≤（
）
x-2，求函数y=2
x-2
-x的值域．
∵
2x2+2x≤2-2(x-2)，
∴x
2+x≤4-2x，即x
2+3x-4≤0，得-4≤x≤1．
又∵y=2
x-2
-x是[-4，1]上的增函数，
∴2
-4-2
4≤y≤2-2
-1．
故所求函数y的值域是[-
，
]．
练习册系列答案
相关习题
科目：高中数学
来源：
题型：
已知
2x2+2x≤（
）
x-2，求函数y=2
x-2
-x的值域．
查看答案和解析>>
科目：高中数学
来源：
题型：
已知
2x2+x≤()x-2，则函数y=2
x-2
-x的值域是
．
查看答案和解析>>
科目：高中数学
来源：
题型：
已知2x
2+y
2=1，则2x+y的最大值是( )
A.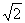
B.2 C.
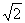D.3
查看答案和解析>>
科目：高中数学
来源：
题型：
已知y=2x+7,则2x
2+y
2的最小值为____________.
查看答案和解析>>
名师指导期末冲刺卷系列答案
