
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)设![]() ,证明:对任意
,证明:对任意![]() ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】我市物价监督部门为调研某公司新开发上市的一种产品销售价格的合理性,对该公司的产品的销售与价格进行了统计分析,得到如下数据和散点图:
定价 | 10 | 20 | 30 | 40 | 50 | 60 |
年销售 | 1150 | 643 | 424 | 262 | 165 | 86 |
| 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
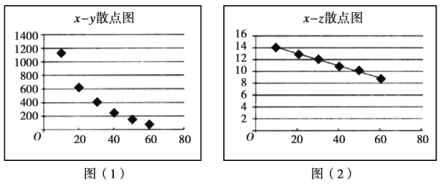
图(1)为![]() 散点图,图(2)为
散点图,图(2)为![]() 散点图.
散点图.
(Ⅰ)根据散点图判断![]() 与
与![]() ,
,![]() 与
与![]() 哪一对具有较强的线性相关性(不必证明);
哪一对具有较强的线性相关性(不必证明);
(Ⅱ)根据(Ⅰ)的判断结果和参考数据,建立![]() 关于
关于![]() 的回归方程(线性回归方程中的斜率和截距均保留两位有效数字);
的回归方程(线性回归方程中的斜率和截距均保留两位有效数字);
(Ⅲ)定价为多少时,年销售额的预报值最大?(注:年销售额![]() 定价
定价![]() 年销售)
年销售)
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)若广告费与销售额具有相关关系,求回归直线方程;
(2)在已有的五组数据中任意抽取两组,求两组数据其预测值与实际值之差的绝对值都不超过5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,C为圆周上一点,过C作圆O的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E. 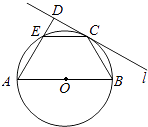
(1)求证:ABDE=BCCE;
(2)若AB=8,BC=4,求线段AE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知![]() ,
,![]() ,动点
,动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求动点![]() 的轨迹方程,并说明曲线
的轨迹方程,并说明曲线![]() 是什么图形;
是什么图形;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)设![]() 是直线
是直线![]() 上的点,过
上的点,过![]() 点作曲线
点作曲线![]() 的切线
的切线![]() ,切点为
,切点为![]() ,设
,设![]() ,求证:过
,求证:过![]() 三点的圆必过定点,并求出所有定点的坐标.
三点的圆必过定点,并求出所有定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px过点P(1,1).过点(0, ![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
(1)求抛物线C的方程,并求其焦点坐标和准线方程;
(2)求证:A为线段BM的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A.1盏
B.3盏
C.5盏
D.9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a>b,a=5,c=6,sinB= ![]() .
.
(Ⅰ)求b和sinA的值;
(Ⅱ)求sin(2A+ ![]() )的值.
)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com