
【题目】如图1,四边形ABCD为矩形,BC=2AB,E为AD的中点,将![]() ABE、
ABE、![]() DCE分别沿BE、CE折起得图2,使得平面
DCE分别沿BE、CE折起得图2,使得平面![]() 平面BCE,平面
平面BCE,平面![]() 平面BCE.
平面BCE.
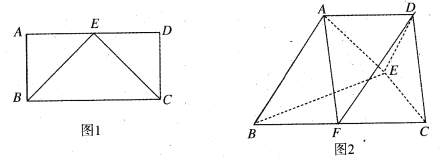
(1)求证:平面![]() 平面DCE;
平面DCE;
(2)若F为线段BC的中点,求直线FA与平面ADE所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)证明![]() 平面ABE,平面
平面ABE,平面![]() 平面DCE即得证;
平面DCE即得证;
(2)以点E为坐标原点,EB,EC所在的直线分别为![]() 轴,
轴,![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设![]() ,利用向量法求直线FA与平面ADE所成角的正弦值得解.
,利用向量法求直线FA与平面ADE所成角的正弦值得解.
(1)证明:在图1中,BC=2AB,且E为AB的中点,
![]()
![]() ,同理
,同理![]() .
.
所以![]() ,
,
又平面![]() 平面BCE,平面
平面BCE,平面![]() 平面
平面![]() ,
,
所以![]() 平面ABE,又
平面ABE,又![]() 平面
平面![]() ,
,
所以平面![]() 平面DCE.
平面DCE.
(2)
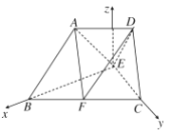
如图,以点E为坐标原点,EB,EC所在的直线分别为![]() 轴,
轴,![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设![]() ,
,
则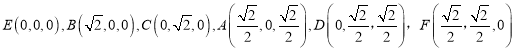 .
.
向量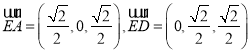 ,设平面ADE的法向量为
,设平面ADE的法向量为![]()
由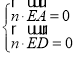 ,得
,得![]() ,令
,令![]() ,
,
得平面ADE的一个法向量为![]() ,
,
又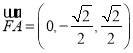 ,
,
设直线FA与平面ADE所成角为![]() ,
,
则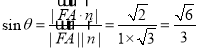
所以直线FA与平面ADE所成角的正弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】《山东省高考改革试点方案》规定:从2017年秋季高中入学的新生开始,不分文理科;2020年开始,高考总成绩由语数外3门统考科目和物理、化学等六门选考科目构成.将每门选考科目的考生原始成绩从高到低划分为A、B+、B、C+、C、D+、D、E共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%.选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100]、[81,90]、[71,80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八个分数区间,得到考生的等级成绩.
某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布N(60,169).
(Ⅰ)求物理原始成绩在区间(47,86)的人数;
(Ⅱ)按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间[61,80]的人数,求X的分布列和数学期望.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,政府相关部门引导乡村发展旅游的同时,鼓励农户建设温室大棚种植高品质农作物.为了解某农作物的大棚种植面积对种植管理成本的影响,甲,乙两同学一起收集6家农户的数据,进行回归分折,得到两个回归摸型:模型①:![]() ,模型②:
,模型②: ![]() ,对以上两个回归方程进行残差分析,得到下表:
,对以上两个回归方程进行残差分析,得到下表:
种植面积 | 2 | 3 | 4 | 5 | 7 | 9 | |
每亩种植管理成本 | 25 | 24 | 21 | 22 | 16 | 14 | |
模型① | 估计值 | 25.27 | 23.62 | 21.97 | 17.02 | 13.72 | |
残差 | -0.27 | 0.38 | -0.97 | -1.02 | 0.28 | ||
模型② |
| 26.84 | 20.17 | 18.83 | 17.31 | 16.46 | |
| -1.84 | 0.83 | 3.17 | -1.31 | -2.46 | ||
(1)将以上表格补充完整,并根据残差平方和判断哪个模型拟合效果更好;
(2)视残差![]() 的绝对值超过1.5的数据视为异常数据,针对(1)中拟合效果较好的模型,剔除异常数据后,重新求回归方程.
的绝对值超过1.5的数据视为异常数据,针对(1)中拟合效果较好的模型,剔除异常数据后,重新求回归方程.
附: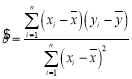 ,
,![]() ;
;![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,我国老年人口比例不断上升,造成日趋严峻的人口老龄化问题.2019年10月12日,北京市老龄办、市老龄协会联合北京师范大学中国公益研究院发布《北京市老龄事业发展报告(2018)》,相关数据有如下图表.规定年龄在15岁至59岁为“劳动年龄”,具备劳动力,60岁及以上年龄为“老年人”,据统计,2018年底北京市每2.4名劳动力抚养1名老年人.
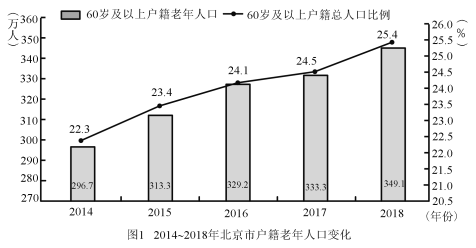
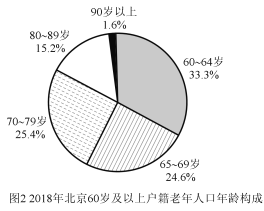
(Ⅰ)请根据上述图表计算北京市2018年户籍总人口数和北京市2018年的劳动力数;(保留两位小数)
(Ⅱ)从2014年起,北京市老龄人口与年份呈线性关系,比照2018年户籍老年人人口年龄构成,预计到2020年年底,北京市90以上老人达到多少人?(精确到1人)
(附:对于一组数据![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: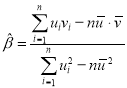 ,
,![]() .
.![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )

A.28B.56C.84D.120
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com