
| A�� | 21 | B�� | 9 | C�� | 5 | D�� | 0 |
���� ��$\overrightarrow{QC}=��\overrightarrow{QA}+��1-�ˣ�\overrightarrow{QB}$���ˡ�R��������A��B��C���ߣ������������������$\overrightarrow{BA}=\overline{PA}-\overrightarrow{PB}$��$\overrightarrow{2PC}=\overrightarrow{PA}+\overrightarrow{PB}$⇒${\overrightarrow{BA}}^{2}={\overrightarrow{PA}}^{2}+{\overrightarrow{PB}}^{2}-2\overrightarrow{PA}•\overrightarrow{PB}$���٣�$4{\overrightarrow{PC}}^{2}={\overrightarrow{PA}}^{2}+{\overrightarrow{PB}}^{2}+2\overrightarrow{PA}•\overrightarrow{PB}$���ڣ�
��-�ٵ�$\overrightarrow{PA}•\overrightarrow{PB}={\overrightarrow{PC}}^{2}-\frac{1}{4}{\overrightarrow{BA}}^{2}$=${\overrightarrow{PC}}^{2}-4$�����PC��Χ���ɣ�
��� �⣺�߶�ƽ���������Q����$\overrightarrow{QC}=��\overrightarrow{QA}+��1-�ˣ�\overrightarrow{QB}$���ˡ�R��������A��B��C���ߣ���ABΪԲC��ֱ����
��$\overrightarrow{BA}=\overline{PA}-\overrightarrow{PB}$��$\overrightarrow{2PC}=\overrightarrow{PA}+\overrightarrow{PB}$⇒${\overrightarrow{BA}}^{2}={\overrightarrow{PA}}^{2}+{\overrightarrow{PB}}^{2}-2\overrightarrow{PA}•\overrightarrow{PB}$���٣�$4{\overrightarrow{PC}}^{2}={\overrightarrow{PA}}^{2}+{\overrightarrow{PB}}^{2}+2\overrightarrow{PA}•\overrightarrow{PB}$���ڣ�
��-�ٵ�$\overrightarrow{PA}•\overrightarrow{PB}={\overrightarrow{PC}}^{2}-\frac{1}{4}{\overrightarrow{BA}}^{2}$=${\overrightarrow{PC}}^{2}-4$��
�ߵ�C��ֱ��ֱ��l2�ľ���Ϊ3����${\overrightarrow{PC}}^{2}��9$����$\overrightarrow{PA}•\overrightarrow{PB}$����СֵΪ5��
��ѡ��C��
���� ���⿼�����������������㣬���ν�ϡ�ת��˼���ǹؼ�������ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{2\sqrt{6}}{5}$ | B�� | -2$\sqrt{6}$ | C�� | 2$\sqrt{6}$ | D�� | $\frac{2\sqrt{6}}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
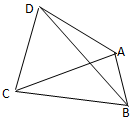 ��ͼ��ʾ����ƽ���ı���ABCD�У�AB=1��BC=2����ACDΪ�������Σ����BCD��������ֵΪ��������
��ͼ��ʾ����ƽ���ı���ABCD�У�AB=1��BC=2����ACDΪ�������Σ����BCD��������ֵΪ��������| A�� | 2 | B�� | $\sqrt{5}$ | C�� | $\sqrt{2}+1$ | D�� | $\sqrt{3}+1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ∅ | B�� | {x|0��x��3} | C�� | {x|1��x��3} | D�� | {x|2��x��3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��5��10�� | B�� | ��-�ޣ�5�� | C�� | ��10��+�ޣ� | D�� | ��-�ޣ�5���ȣ�10��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com