
| ||
| 2 |
| ||
| 2 |
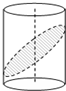 解:设圆柱的底面直径为2a,所以由意可得椭圆的短轴长是20a,
解:设圆柱的底面直径为2a,所以由意可得椭圆的短轴长是20a,
| 3 |
| ||
| 2 |
| ||
| 2 |


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
 如图,在平面直角坐标系中.锐角α,β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系中.锐角α,β的终边分别与单位圆交于A,B两点.| 3 |
| 4 |
| 5 |
| 13 |
查看答案和解析>>
科目:高中数学 来源:全优设计选修数学-1-1苏教版 苏教版 题型:044
我们知道,圆是平面内到定点的距离等于定长的点的轨迹,因此可以判断一点与一个圆的位置关系——当该点到圆心的距离等于半径时,该点在该圆上;当该点到圆心的距离小于半径时,该点在该圆内;当该点到圆心的距离大于半径时,该点在该圆上外.你能根据椭圆的定义来判断一个点相对于一个椭圆的位置关系吗?如果能,应该如何判断?
查看答案和解析>>
科目:高中数学 来源:设计选修数学-1-1苏教版 苏教版 题型:044
我们知道,圆是平面内到定点的距离等于定长的点的轨迹,由此可以判断一点与一个圆的位置关系——当该点到圆心的距离等于半径时,该点在该圆上;当该点到圆心的距离小于半径时,该点在该圆内;当该点到圆心的距离大于半径时,该点在该圆外.你能根据椭圆的定义来判断一个点相对于一个椭圆的位置关系吗?如果能,应该如何判断?
查看答案和解析>>
科目:高中数学 来源:选修设计数学1-1北师大版 北师大版 题型:044
我们知道,圆是平面内到定点的距离等于定长的点的轨迹,由此可以判断一点与一个圆的位置关系——当该点到圆心的距离等于半径时,该点在该圆上;当该点到圆心的距离小于半径时,该点在该圆内;当该点到圆心的距离大于半径时,该点在该圆外.你能根据椭圆的定义来判断一个点相对于一个椭圆的位置关系吗?如果能,应该如何判断?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com