
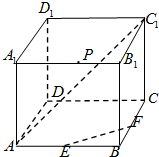
 在长方体ABCD-A1B1C1D1中,AB=AA1=4,BC=3,E、F分别是所在棱AB、BC的中点,点P是棱A1B1上的动点,联结EF,AC1.如图所示.
在长方体ABCD-A1B1C1D1中,AB=AA1=4,BC=3,E、F分别是所在棱AB、BC的中点,点P是棱A1B1上的动点,联结EF,AC1.如图所示.| AE |
| AF |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
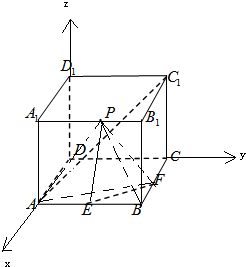 解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,
解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,| 3 |
| 2 |
| EF |
| 3 |
| 2 |
| AC1 |
| EF |
| AC1 |
| ||||||
|
5
| ||
| 41 |
5
| ||
| 41 |
| AE |
| AF |
| 3 |
| 2 |
| AE |
| AF |
| ||
| 2 |
| AE |
| AF |
| 8 | ||||
2×
|
8
| ||
| 73 |
| AE |
| AF |
1-(
|
3
| ||
| 73 |
| 1 |
| 2 |
| AE |
| AF |
| AE |
| AF |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 73 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |


科目:高中数学 来源: 题型:
| A、12 | B、10 | C、8 | D、6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 随着经济的发展,到某岛进行旅游观光的人数越来越多,交通问题已成为制约经济发展的重要因素,因此政府欲在大陆和岛屿之间(如图)建立一条高速通道以便于大陆和岛屿之间来往,大陆沿海线可近似看作函数f(x)=ax(a>1)的图象,且正好与直线y=x相切,而岛屿海岸线可近似看作函数g(x)=loga(x-3)(a>1)的图象.(每单位代表十万米)
随着经济的发展,到某岛进行旅游观光的人数越来越多,交通问题已成为制约经济发展的重要因素,因此政府欲在大陆和岛屿之间(如图)建立一条高速通道以便于大陆和岛屿之间来往,大陆沿海线可近似看作函数f(x)=ax(a>1)的图象,且正好与直线y=x相切,而岛屿海岸线可近似看作函数g(x)=loga(x-3)(a>1)的图象.(每单位代表十万米)查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面ABCD是边长为
如图,在四棱锥P-ABCD中,底面ABCD是边长为| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| e |
| f(x) |
| x2 |
| ln2 |
| 24 |
| ln3 |
| 34 |
| lnn |
| n4 |
| 1 |
| 2e |
查看答案和解析>>
科目:高中数学 来源: 题型:

| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com