
【题目】己知函数![]() .
.
(1)试讨论f(x)的单调性;
(2)若函数![]() 有且只有三个不同的零点,分别记为x1,x2,x3,设x1<x2<x3,且
有且只有三个不同的零点,分别记为x1,x2,x3,设x1<x2<x3,且![]() 的最大值是e2,求x1x3的最大值.
的最大值是e2,求x1x3的最大值.
【答案】(1)当m≤0时,函数![]() 在区间(0,+∞)上单调递增;当m>0时, 函数
在区间(0,+∞)上单调递增;当m>0时, 函数![]() 在(0,
在(0,![]() )上单调递增,函数
)上单调递增,函数![]() 在(
在(![]() ,+∞)上单调递减;(2)
,+∞)上单调递减;(2)![]() .
.
【解析】
(1)求出函数的导数,对m分类讨论,解得导函数大于0及小于0的范围,即可得到单调性.
(2)由条件可将问题转化函数y=m的图象与函数![]() 的图象有两个交点.分析可得0<x1<e,x3>e.令
的图象有两个交点.分析可得0<x1<e,x3>e.令![]() ,则t∈
,则t∈![]() .由
.由 ,解得
,解得 构造
构造![]() ,t∈
,t∈![]() ,利用导函数转化求解即可.
,利用导函数转化求解即可.
(1)函数的定义域为(0,+∞).
由已知可得![]() .
.
当m≤0时,![]() >0,故
>0,故![]() 在区间(0,+∞)上单调递增;
在区间(0,+∞)上单调递增;
当m>0时,由![]() >0,解得
>0,解得![]() ;由
;由![]() 0,解得
0,解得![]() .
.
所以函数![]() 在(0,
在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减.
,+∞)上单调递减.
综上所述,当m≤0时,函数![]() 在区间(0,+∞)上单调递增;
在区间(0,+∞)上单调递增;
当m>0时, 函数![]() 在(0,
在(0,![]() )上单调递增,
)上单调递增,
函数![]() 在(
在(![]() ,+∞)上单调递减.
,+∞)上单调递减.
(2)∵ 函数g(x)=(x-e)(lnx-mx)有且只有三个不同的零点,
显然x=e是其零点,
∴ 函数![]() 存在两个零点,即
存在两个零点,即![]() 有两个不等的实数根.
有两个不等的实数根.
可转化为方程![]() 在区间(0,+∞)上有两个不等的实数根,
在区间(0,+∞)上有两个不等的实数根,
即函数y=m的图象与函数![]() 的图象有两个交点.
的图象有两个交点.
∵ ![]() ,
,
∴ 由![]() >0,解得
>0,解得![]() ,故
,故![]() 在上单调递增;
在上单调递增;
由![]() <0,解得x>e,故
<0,解得x>e,故![]() 在(e,+∞)上单调递减;
在(e,+∞)上单调递减;
故函数y=m的图象与![]() 的图象的交点分别在(0,e),(e,+∞)上,
的图象的交点分别在(0,e),(e,+∞)上,
即lnx-mx=0的两个根分别在区间(0,e),(e,+∞)上,
∴ g(x)的三个不同的零点分别是x1,e,x3,且0<x1<e,x3>e.
令![]() ,则t∈
,则t∈![]() .
.
由 ,解得
,解得
故![]() ,t∈
,t∈![]() .
.
令![]() ,则
,则![]() .
.
令![]() ,则
,则![]() .
.
所以![]() 在区间
在区间![]() 上单调递增,即
上单调递增,即![]() >
>![]() .
.
所以![]() ,即
,即![]() 在区间
在区间![]() 上单调递增,
上单调递增,
即![]() ≤
≤![]() =
=![]() ,
,
所以![]() ,即x1x3≤
,即x1x3≤![]() ,
,
所以x1x3的最大值为![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】下列结论正确的有( )
A.公共汽年上有10位乘客,沿途5个车站,乘客下车的可能方式有![]() 种.
种.
B.两位男生和两位女生随机排成一列,则两位女生不相邻的概率是![]() ;
;
C.若随机変量![]() 服从二项分布
服从二项分布![]() ,则
,则![]() ;
;
D.已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11,若这组数据的平均数、中位数,众数依次成等差数列,则丢失数据的所有可能值的和为12.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李庄村某社区电费收取有以下两种方案供农户选择:
方案一:每户每月收管理费2元,月用电不超过30度,每度0.4元,超过30度时,超过部分按每度0.5元.
方案二:不收管理费,每度0.48元.
(1)求方案一收费![]() 元与用电量
元与用电量![]() (度)间的函数关系;
(度)间的函数关系;
(2)小李家九月份按方案一交费34元,问小李家该月用电多少度?
(3)小李家月用电量在什么范围时,选择方案一比选择方案二更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进入冬天,大气流动性变差,容易形成雾握天气,从而影响空气质量.某城市环保部门试图探究车流量与空气质量的相关性,以确定是否对车辆实施限行.为此,环保部门采集到该城市过去一周内某时段车流量与空气质量指数的数据如下表:

(1)根据表中周一到周五的数据,求y关于x的线性回归方程。
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2,则认为得到的线性回归方程是可靠的.请根据周六和周日数据,判定所得的线性回归方程是否可靠?
注:回归方程![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为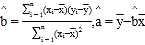 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (
(![]() ,
,![]() ),
),![]() ,
,![]() 是双曲线的两个顶点,
是双曲线的两个顶点,![]() 是双曲线上的一点,且与点
是双曲线上的一点,且与点![]() 在双曲线的同一支上,
在双曲线的同一支上,![]() 关于
关于![]() 轴的对称点是
轴的对称点是![]() ,若直线
,若直线![]() ,
,![]() 的斜率分别是
的斜率分别是![]() ,
,![]() ,且
,且![]() ,则双曲线的离心率是( )
,则双曲线的离心率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有12个球,颜色、大小完全一样,在重量上,其中一个球不合格,但不知这个球比标准的重还是轻.能否在一架天平上只称三次(不用砝码),把这个不合格的球找出来?
查看答案和解析>>
科目:高中数学 来源: 题型:
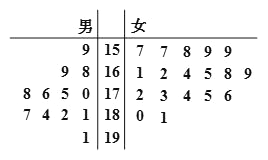
【题目】某学校在学校内招募了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者.将这
名女志愿者.将这![]() 名志愿者的身高编成如右茎叶图(单位:
名志愿者的身高编成如右茎叶图(单位: ![]() ),若身高在
),若身高在![]() 以上(包括
以上(包括![]() )定义为“高个子”,身高在
)定义为“高个子”,身高在![]() 以下(不包括
以下(不包括![]() )定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
(Ⅰ)如果用分层抽样的方法从“高个子”和“非高个子”中抽取![]() 人,再从这
人,再从这![]() 人中选
人中选![]() 人,那么至少有一人是“高个子”的概率是多少?
人,那么至少有一人是“高个子”的概率是多少?
(Ⅱ)若从所有“高个子”中选![]() 名志愿者,用
名志愿者,用![]() 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一个高为4长方体截去一个角所得的多面体的直观图及它的正(主)视图和侧(左)视图(单位:![]() )
)
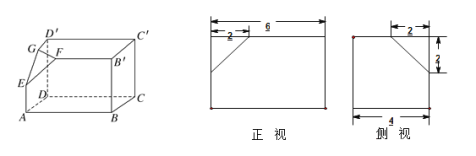
(1)求异面直线![]() 与
与![]() 所成角的余弦;
所成角的余弦;
(2)将求异面直线![]() 与
与![]() 所成的角转化为求一个三角形的内角即可,要求只写出找角过程,不需计算结果;
所成的角转化为求一个三角形的内角即可,要求只写出找角过程,不需计算结果;
(3)求异面直线![]() 与
与![]() 所成的角;要求同(2).
所成的角;要求同(2).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com