
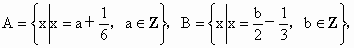
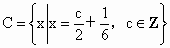 ,则集合A、B、C满足的关系是
,则集合A、B、C满足的关系是
[ ]
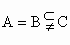

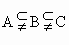
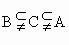
|
写出集合 A、B、C中的所有元素,并进行比较或找出三个集合的共性进行分析.解法 1:简单列举各集合中的元素.
由各集合中的元素可以知道: 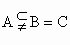 . .
解法 2:判断集合中元素的共性和差异.
∵ 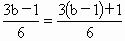 ,而 ,而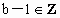 , ,
即 3(b-1)+1与3c+1都表示被3除余1的数,而6a+1表示被6除余1的数,∴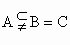 . . |
|
记住如下结论有助于我们今后解决此类问题. (1)一个整数被2整除,记作2k或2k+2,或2k-2,一个整数被2除余1,可记为2k+1或2k-1; (2)一个整数被3整除可记为3k,被3除余1,可记为3k+1或3k-2,被3除余2可记为3k+2或3k-1. (3)一个整数被4整除,可记为4k,被4除余1,可记为4k+1,被4除余2可记为4k+2,被4除余3可记为4k+3或4k-1. |


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:广西桂林十八中2012届高三第一次月考数学文科试题 题型:013
映射f:A→B如果满足集合B中的任意一个元素在A中都有原像,则称为满射,已知集合A中有5个元素,集合B中有3个元素,那么集合A到B的不同满射的个数为
243
240
150
72
查看答案和解析>>
科目:高中数学 来源:广西桂林十八中2012届高三第一次月考数学理科试题 题型:013
映射f:A→B如果满足集合B中的任意一个元素在A中都有原像,则称为满射,已知集合A中有5个元素,集合B中有3个元素,那么集合A到B的不同满射的个数为
243
240
150
72
查看答案和解析>>
科目:高中数学 来源: 题型:
映射f:A→B,如果满足集合B中的任意一个元素在A中都有原象,则称为“满射”. 已知集合A中有4个元素,集合B中有3个元素,那么从A到B的不同满射的个数为( )
A.24 B.
查看答案和解析>>
科目:高中数学 来源:2014届江西省高二第一次月考理科数学试卷(解析版) 题型:选择题
映射f:A→B,如果满足集合B中的任意一个元素在A中都有原象,则称为“满射”.已知集合A中有4个元素,集合B中有3个元素,那么从A到B的不同满射的个数为
A.24 B.6 C. 36 D.72
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省湛江市高三8月第一次月考理科数学试卷(解析版) 题型:选择题
已知映射 ,其中集合
,其中集合 ,若对于
,若对于 ,都有
,都有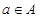 使得
使得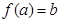 成立,称该映射为从集合
成立,称该映射为从集合 到集合
到集合 的一个“满射”。则从集合
的一个“满射”。则从集合 到集合
到集合 可以建立(
)个“满射”。
可以建立(
)个“满射”。
A.18 B.36 C.64 D.81
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com