【题目】已知动点
到直线
的距离比到点
的距离大
（1）求动点的轨迹
的方程；
（2）
为上两点，
为坐标原点，
，过分别作的两条切线，相交于点
，求
面积的最小值.
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案科目：高中数学 来源： 题型：
【题目】已知直线
与椭圆
交于不同的两点
，
.
（1）若线段
的中点为
，求直线的方程；
（2）若的斜率为
，且过椭圆
的左焦点
，的垂直平分线与
轴交于点
，求证：
为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，三棱柱
中，
侧面
，已知
，
，
，点
是棱
的中点.
（1）求证：
平面
；
（2）求二面角
的余弦值；
（3）在棱
上是否存在一点
，使得
与平面
所成角的正弦值为
，若存在，求出
的值；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线L：
（
）的焦点为F，过点
的动直线l与抛物线L交于A，B两点，直线
交抛物线L于另一点C，直线
的最小值为4.
（1）求椭圆C的方程；
（2）若过点A作y轴的垂线m，则x轴上是否存在一点
，使得直线PB与直线m的交点恒在一条定直线上？若存在，求该点的坐标及该定直线的方程；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】小姜同学有两个盒子
和
，最初盒子有6枚硬币，盒子是空的.在每一回合中，她可以将一枚硬币从盒移到盒，或者从盒移走
枚硬币，其中是盒中当前的硬币数.当盒空时她获胜.则小姜可以获胜的最少回合是( )
A.三回合B.四回合C.五回合D.六回合
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某企业有甲、乙两套设备生产同一种产品，为了检测两套设备的生产质量情况，随机从两套设备生产的大量产品中各抽取了50件产品作为样本，检测一项质量指标值，若该项质量指标值落在
内，则为合格品，否则为不合格品. 表1是甲套设备的样本的频数分布表，图1是乙套设备的样本的频率分布直方图.
表1：甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 5 | 18 | 19 | 6 | 1 |
图1：乙套设备的样本的频率分布直方图
（Ⅰ）将频率视为概率. 若乙套设备生产了5000件产品，则其中的不合格品约有多少件；
（Ⅱ）填写下面列联表，并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关；
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
（Ⅲ）根据表1和图1，对两套设备的优劣进行比较.
附：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系 xOy 中，已知椭圆 C：
＝1(a>b>0)的离心率为
，且过点
，点P在第四象限， A为左顶点， B为上顶点， PA交y轴于点C，PB交x轴于点D.
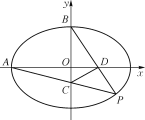
(1) 求椭圆 C 的标准方程；
(2) 求 △PCD 面积的最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
