
【题目】方舱医院的启用在本次武汉抗击新冠疫情的关键时刻起到了至关重要的作用,图1为某方舱医院的平面设计图,其结构可以看成矩形在四个角处对称地截去四个全等的三角形所得,图2中所示多边形![]() ,整体设计方案要求:内部井字形的两根水平横轴
,整体设计方案要求:内部井字形的两根水平横轴![]() 米,两根竖轴
米,两根竖轴![]() 米,记整个方舱医院的外围隔离线(图2实线部分,轴和边框的粗细忽略不计)总长度为
米,记整个方舱医院的外围隔离线(图2实线部分,轴和边框的粗细忽略不计)总长度为![]() ,
,![]() 与
与![]() 、
、![]() 的交点为
的交点为![]() 、
、![]() ,
,![]() 与
与![]() 、
、![]() 的交点为
的交点为![]() 、
、![]() ,
,![]() (
(![]() ).
).

(1)若![]() ,且两根横轴之间的距离
,且两根横轴之间的距离![]() 米,求外围隔离线总长度
米,求外围隔离线总长度![]() ;
;
(2)由于疫情需要,外围隔离线总长度![]() 不超过240米,当整个方舱医院(多边形
不超过240米,当整个方舱医院(多边形![]() 的面积)最大时,给出此设计方案中
的面积)最大时,给出此设计方案中![]() 的大小与
的大小与![]() 的长度.
的长度.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】中国古代几何中的勾股容圆,是阐述直角三角形中内切圆问题. 此类问题最早见于《九章算术》“勾股”章,该章第16题为:“今有勾八步,股十五步. 问勾中容圆,径几何?”意思是“直角三角形的两条直角边分别为8和15,则其内切圆直径是多少?”若向上述直角三角形内随机抛掷120颗米粒(大小忽略不计,取![]() ),落在三角形内切圆内的米粒数大约为( )
),落在三角形内切圆内的米粒数大约为( )
A.54B.48C.42D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京2022年冬奥会和冬残奥会色彩系统的主色包括霞光红迎春黄天霁蓝长城灰瑞雪白;间色包括天青梅红竹绿冰蓝吉柿;辅助色包括墨金银.若各赛事纪念品的色彩设计要求:主色至少一种至多两种,间色两种辅助色一种,则某个纪念品的色彩搭配中包含有瑞雪白冰蓝银色这三种颜色的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C :![]() 与圆
与圆![]() 相交于M,N,P,Q四点,四边形MNPQ为正方形,△PF1F2的周长为
相交于M,N,P,Q四点,四边形MNPQ为正方形,△PF1F2的周长为![]()
(1)求椭圆C的方程;
(2)设直线l与椭圆C相交于A、B两点![]() 若直线AD与直线BD的斜率之积为
若直线AD与直线BD的斜率之积为![]() ,证明:直线恒过定点.
,证明:直线恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记无穷数列![]() 的前n项
的前n项![]() ,
,![]() ,…,
,…,![]() 的最大项为
的最大项为![]() ,第n项之后的各项
,第n项之后的各项![]() ,
,![]() ,…的最小项为
,…的最小项为![]() ,
,![]() .
.
(1)若数列![]() 的通项公式为
的通项公式为![]() ,写出
,写出![]() ,
,![]() ,
,![]() ;
;
(2)若数列![]() 的通项公式为
的通项公式为![]() ,判断
,判断![]() 是否为等差数列,若是,求出公差;若不是,请说明理由;
是否为等差数列,若是,求出公差;若不是,请说明理由;
(3)若数列![]() 为公差大于零的等差数列,求证:
为公差大于零的等差数列,求证:![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”,将上述问题的所有正整数答案从小到大组成一个数列![]() ,则
,则![]() ______;
______;![]() ______.(注:三三数之余二是指此数被3除余2,例如“5”)
______.(注:三三数之余二是指此数被3除余2,例如“5”)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数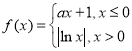 ,给出下列三个结论:
,给出下列三个结论:
①当![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ;
;
②若函数![]() 无最小值,则
无最小值,则![]() 的取值范围为
的取值范围为![]() ;
;
③若![]() 且
且![]() ,则
,则![]() ,使得函数
,使得函数![]() .恰有3个零点
.恰有3个零点![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
其中,所有正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是通过自助结算方式购物的一种形式. 某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 |
|
|
|
|
| 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取 1 名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com