
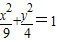 的下顶点为C,A,B分别在椭圆的第一象限和第二象限的弧上运动,满足
的下顶点为C,A,B分别在椭圆的第一象限和第二象限的弧上运动,满足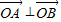 ,其中O为坐标原点,现沿x轴将坐标平面折成直二面角.如图2所示,在空间中,解答下列问题:
,其中O为坐标原点,现沿x轴将坐标平面折成直二面角.如图2所示,在空间中,解答下列问题: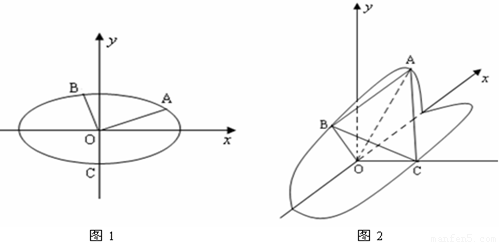
 ,OA⊥OB,设直线OA方程为y=kx,OB的方程为y=-
,OA⊥OB,设直线OA方程为y=kx,OB的方程为y=- ,解方程组
,解方程组 ,得A(
,得A( ,
, ),解方程组
),解方程组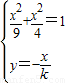 ,得B(-
,得B(-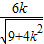 ,
, ),
),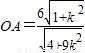 ,OB=
,OB=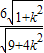 ,OC=2,以O为原点,以OA为x轴,OB为y轴,OC为z轴,建立空间直角坐标系,由向量法能够证明cos2α+cos2β+cos2θ=1.
,OC=2,以O为原点,以OA为x轴,OB为y轴,OC为z轴,建立空间直角坐标系,由向量法能够证明cos2α+cos2β+cos2θ=1.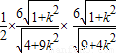 =
=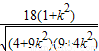 ≥3,由此能求出三棱锥O-ABC的体积的最小值.
≥3,由此能求出三棱锥O-ABC的体积的最小值. ,∴OA⊥OB,
,∴OA⊥OB,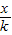 ,
,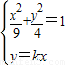 ,得A(
,得A( ,
,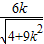 ),(舍去x<0的解)
),(舍去x<0的解) ,得B(-
,得B(- ,
, ),(舍去x>0的解)
),(舍去x>0的解) ,OB=
,OB= ,OC=2,
,OC=2, ),B(0,
),B(0, ,0),C(0,0,2),
,0),C(0,0,2),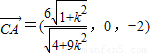 ,
,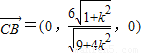 ,
,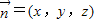 ,则有
,则有 ,
, ,
, ,
, =
= ,
, ,
,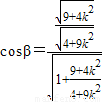 ,
,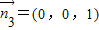 ,
,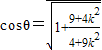 ,
,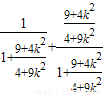 =1.
=1. =
= ≥3,
≥3, .
.

科目:高中数学 来源:2013届江苏省高二第二次月考数学试卷 题型:解答题
(本小题满分16分) 如图,设椭圆 的右顶点与上顶点分别
的右顶点与上顶点分别
为A、B,以A为圆心,OA为半径的圆与以B为圆心,OB为半径的圆相交于点O、P.
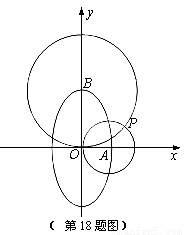
(1)求点P的坐标;
(2) 若点P在直线 上,求椭圆的离心率;
上,求椭圆的离心率;
(3) 在(2)的条件下,设M是椭圆上的一动点,且点N(0,1)到椭圆上点的最近距离为3,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省徐州市丰县修远双语学校高二(上)第二次月考数学试卷(解析版) 题型:解答题
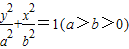 的右顶点与上顶点分别为A、B,以A为圆心,OA为半径的圆与以B为圆心,OB为半径的圆相交于点O、P.
的右顶点与上顶点分别为A、B,以A为圆心,OA为半径的圆与以B为圆心,OB为半径的圆相交于点O、P.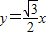 上,求椭圆的离心率;
上,求椭圆的离心率;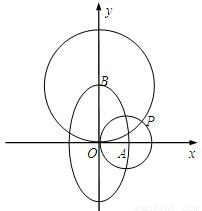
查看答案和解析>>
科目:高中数学 来源:2010年山东省青岛二中高考数学预测试卷2(文科)(解析版) 题型:解答题
 的右顶点与上顶点分别为A、B,以A为圆心,OA为半径的圆与以B为圆心,OB为半径的圆相交于点O、P.
的右顶点与上顶点分别为A、B,以A为圆心,OA为半径的圆与以B为圆心,OB为半径的圆相交于点O、P. 上,求椭圆的离心率;
上,求椭圆的离心率;
查看答案和解析>>
科目:高中数学 来源:2010年江苏省南通市海安中学高三学情分析数学试卷(理科)(解析版) 题型:解答题
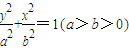 的右顶点与上顶点分别为A、B,以A为圆心,OA为半径的圆与以B为圆心,OB为半径的圆相交于点O、P.
的右顶点与上顶点分别为A、B,以A为圆心,OA为半径的圆与以B为圆心,OB为半径的圆相交于点O、P.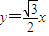 上,求椭圆的离心率;
上,求椭圆的离心率;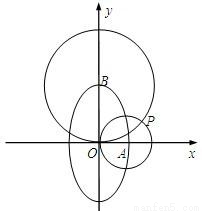
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com