
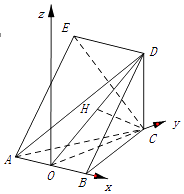
【题目】如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°, ![]() .
. 
(1)证明:DC⊥AB;
(2)若点C在平面ABDE内的射影H,求CH与平面BCD所成的角的正弦值.
【答案】
(1)证明:如图,取AB的中点O,连OC,OD,
因为△ABC是边长为2的正三角形,所以 ![]() ,
,
又四边形ABDE是菱形,∠DBA=60°,所以△DAB是正三角形,
所以 ![]() ,
,
而OD∩OC=O,所以AB⊥平面DOC,
所以AB⊥CD.
(2)解:由(1)知OC=CD,平面DOC⊥平面ABD,
因为平面DOC与平面ABD的交线为OD,
所以点C在平面ABDE内的射影H必在OD上,
所以H是OD的中点,
如图所示建立空间直角坐标系O﹣xyz, ![]() ,
, ![]() ,
,
所以 ![]() ,
, ![]() ,
, ![]() ,
,
设平面BDC的法向量为 ![]() ,则
,则 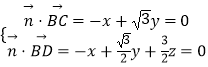 ,取
,取 ![]() ,则x=3,z=1,
,则x=3,z=1,
即平面BCD的一个法向量为 ![]() .
.
所以CH与平面BCD所成的角的正弦值为 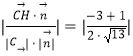 =
= ![]() .
.
【解析】(1)取AB的中点O,连OC,OD,证明:AB⊥平面DOC,即可证明DC⊥AB;(2)若点C在平面ABDE内的射影H,建立空间直角坐标系,利用向量方法求CH与平面BCD所成的角的正弦值.
【考点精析】根据题目的已知条件,利用空间中直线与直线之间的位置关系和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则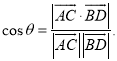 .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】设函数 f(x)=|x+2|﹣|x﹣3|﹣a
(Ⅰ)当 a=1 时,求函数 f(x)的最大值;
(Ⅱ)若 f(x)≤ ![]() 对任意 x∈R 恒成立,求实数 a 的取值范围.
对任意 x∈R 恒成立,求实数 a 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有人用三段论进行推理:“函数![]() 的导函数
的导函数![]() 的零点即为函数
的零点即为函数![]() 的极值点,函数
的极值点,函数![]() 的导函数的零点为
的导函数的零点为![]() ,所以
,所以![]() 是函数
是函数![]() 的极值点 ”,上面的推理错误的是( )
的极值点 ”,上面的推理错误的是( )
A. 大前提 B. 小前提 C. 推理形式 D. 以上都是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体ABCD﹣A1B1C1D1的棱长为1,点E,F分别是棱D1C1 , B1C1的中点,过E,F作一平面α,使得平面α∥平面AB1D1 , 则平面α截正方体的表面所得平面图形为( )
A.三角形
B.四边形
C.五边形
D.六边形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代第一部数学专著,成于公元一世纪左右,系统总结了战国、秦、汉时期的数学成就.其中《方田》一章中记载了计算弧田(弧田就是由圆弧和其所对弦所围成弓形)的面积所用的经验公式:弧田面积=![]() (弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为
(弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为![]() ,弦长为
,弦长为![]() 的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中
的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中![]() ,
,![]() )
)
A. 15 B. 16 C. 17 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆 ![]() 的离心率为
的离心率为 ![]() ,顶点为A1、A2、B1、B2 , 且
,顶点为A1、A2、B1、B2 , 且 ![]() .
.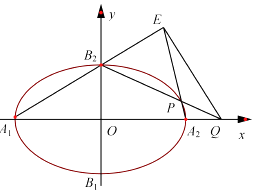
(1)求椭圆C的方程;
(2)P是椭圆C上除顶点外的任意点,直线B2P交x轴于点Q,直线A1B2交A2P于点E.设A2P的斜率为k,EQ的斜率为m,试问2m﹣k是否为定值?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com