
【题目】已知函数 ![]() .
.
(1)求函数f(x)的定义域;
(2)求f(1),f(﹣1),f(2),f(﹣2);
(3)判断并证明f(x)的奇偶性.
【答案】
(1)解:由2x﹣1≠0,解得x≠0.
∴函数f(x)的定义域为(﹣∞,0)∪(0,+∞)
(2)解:f(1)= ![]() ,f(﹣1)=
,f(﹣1)= ![]() ,
,
f(2)= ![]() ,f(﹣2)=
,f(﹣2)= ![]() =﹣
=﹣ ![]()
(3)解:函数 ![]() 为定义域内的奇函数.
为定义域内的奇函数.
证明如下:函数f(x)的定义域为(﹣∞,0)∪(0,+∞).
∵ ![]() =
= ![]() .
.
f(﹣x)= 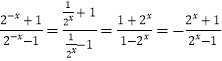 =﹣f(x).
=﹣f(x).
∴函数 ![]() 为定义域内的奇函数
为定义域内的奇函数
【解析】(1)根据分式有意义及指数的运算求得函数的定义域;(2)一般计算,需要注意指数的运算即可;(3)根据奇偶函数的定义来判断,化简过程需要认真计算.
【考点精析】本题主要考查了函数的定义域及其求法和函数的奇偶性的相关知识点,需要掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;偶函数的图象关于y轴对称;奇函数的图象关于原点对称才能正确解答此题.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;偶函数的图象关于y轴对称;奇函数的图象关于原点对称才能正确解答此题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】随机抽取某班6名学生,测量他们的身高(单位:cm),获得身高数据依次为:162,168,170,171,179,182,那么此班学生平均身高大约为cm;样本数据的方差为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产三种型号的轿车,产量分别是1600辆、6000辆和2000辆,为检验公司的产品质量,现从这三种型号的轿车种抽取48辆进行检验,这三种型号的轿车依次应抽取 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知双曲线 ![]() (a>0,b>0)的左、右焦点分别为F1、F2 , |F1F2|=8,P是双曲线右支上的一点,直线F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=2,则该双曲线的离心率为( )
(a>0,b>0)的左、右焦点分别为F1、F2 , |F1F2|=8,P是双曲线右支上的一点,直线F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=2,则该双曲线的离心率为( ) 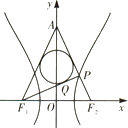
A.![]()
B.![]()
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|0≤x≤2},B={y|1≤y≤2},若对于函数y=f(x),其定义域为A,值域为B,则这个函数的图象可能是( )
A.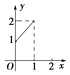
B.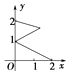
C.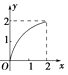
D.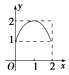
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= ![]() AD=1,CD=
AD=1,CD= ![]() .
. 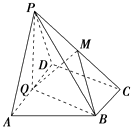
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M﹣QB﹣C为30°,求线段PM与线段MC的比值t.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,其中a>0.
,其中a>0.
(Ⅰ)当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求f(x)在区间[1,e]上的最小值.(其中e是自然对数的底数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com