
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(Ⅰ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅱ)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
【答案】(Ⅰ)当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ;
; ![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ;(Ⅱ)0.
;(Ⅱ)0.
【解析】试题分析:(Ⅰ)先求函数的导函数,原函数的单调增区间即为使导函数大于零的区间,根据导函数分段讨论![]() 的不同取值范围时的单调增区间即可.
的不同取值范围时的单调增区间即可.
(Ⅱ)![]() 单调递增,存在唯一
单调递增,存在唯一![]() ,使得
,使得![]() ,即
,即![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,所以
,所以![]()
![]() 求得
求得![]() 的范围,得到
的范围,得到![]() 的范围,得到
的范围,得到![]() 最小整数值.
最小整数值.
试题解析:(Ⅰ) ![]()
![]()
![]() (
(![]() )
)
①当![]() 时,由
时,由![]() ,解得
,解得![]() ;
;
②当![]() 时,由
时,由![]() ,解得
,解得![]() ;
;
③当![]() 时,由
时,由![]() ,解得
,解得![]() ;
;
综上所述,
当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ;
;
![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() .
.
(Ⅱ)当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() 单调递增,
单调递增, ![]()
![]() ,
, ![]()
![]() ,
,
所以存在唯一![]() ,使得
,使得![]() ,即
,即![]() ,
,
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以![]()
![]()
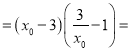
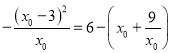 ,
,
记函数![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() ,
,
由![]() ,且
,且![]() 为整数,得
为整数,得![]() ,
,
所以存在整数![]() 满足题意,且
满足题意,且![]() 的最小值为0.
的最小值为0.
点晴:本题主要考查导数的单调性,导数与极值点、不等式等知识. 解答此类问题,应该首先确定函数的定义域,否则,写出的单调区间易出错. 解决含参数问题及不等式问题注意两个转化:(1)利用导数解决含有参数的单调性问题可将问题转化为不等式恒成立问题,要注意分类讨论和数形结合思想的应用.(2)将不等式的证明、方程根的个数的判定转化为函数的单调性问题处理.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,离心率等于
的中心在原点,离心率等于![]() ,它的一个短轴端点恰好是抛物线
,它的一个短轴端点恰好是抛物线![]() 的焦点
的焦点
(1)求椭圆![]() 的方程;
的方程;
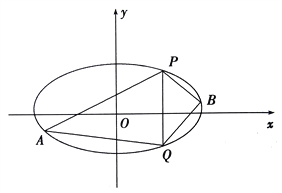
(2)已知![]() 、
、![]() 是椭圆上的两点,
是椭圆上的两点, ![]() ,
, ![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.①若直线
两侧的动点.①若直线![]() 的斜率为
的斜率为![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
②当![]() ,
, ![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由
的斜率是否为定值,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为14分)已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 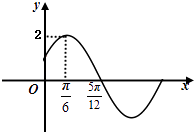
(1)求函数f(x)的解析式;
(2)令g(x)=f(﹣x﹣ ![]() ),求g(x)的单调递增区间.
),求g(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,且a2+bc=b2+c2
(1)求∠A的大小;
(2)若b=2,a= ![]() ,求边c的大小;
,求边c的大小;
(3)若a= ![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com