
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上,![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线l经过点![]() ,且与椭圆
,且与椭圆![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() (
(![]() 为坐标原点)成等比数列,判断直线
为坐标原点)成等比数列,判断直线![]() 的斜率是否为定值?若是,请求出该定值;若不是,请说明理由.
的斜率是否为定值?若是,请求出该定值;若不是,请说明理由.
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠DAB=60°.

(1)证明:AD⊥PB.
(2)若PB=![]() ,AB=PA=2,求三棱锥P-BCD的体积。
,AB=PA=2,求三棱锥P-BCD的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,将
,将![]() 的图象向左平移
的图象向左平移![]() 个单位后,所得图象关于原点对称,则函数
个单位后,所得图象关于原点对称,则函数![]() 的图象( )
的图象( )
A.关于直线![]() 对称B.关于直线
对称B.关于直线![]() 对称
对称
C.关于点(![]() ,0)对称D.关于点(
,0)对称D.关于点(![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
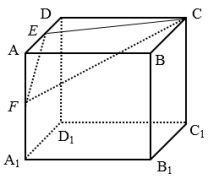
【题目】如图,正方体![]() 的棱长为2,
的棱长为2,![]() 分别为
分别为![]() 的中点,则以下说法错误的是( )
的中点,则以下说法错误的是( )
A.平面![]() 截正方体所的截面周长为
截正方体所的截面周长为![]()
B.存在![]() 上一点
上一点![]() 使得
使得![]() 平面
平面![]()
C.三棱锥![]() 和
和![]() 体积相等
体积相等
D.存在![]() 上一点
上一点![]() 使得
使得![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,河南省郑州市的房价依旧是郑州市民关心的话题.总体来说,二手房房价有所下降,相比二手房而言,新房市场依然强劲,价格持续升高.已知销售人员主要靠售房提成领取工资.现统计郑州市某新房销售人员一年的工资情况的结果如图所示,若近几年来该销售人员每年的工资总体情况基本稳定,则下列说法正确的是( )

A.月工资增长率最高的为8月份
B.该销售人员一年有6个月的工资超过4000元
C.由此图可以估计,该销售人员2020年6,7,8月的平均工资将会超过5000元
D.该销售人员这一年中的最低月工资为1900元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com