
����Ŀ��ij���������˾ÿ��ƻ����������������ɡ����������߹� ![]() ��������һ��������
��������һ�������� ![]() ���ӣ�����һ�������
���ӣ�����һ������� ![]() ���ӣ�����һ��ɡ����
���ӣ�����һ��ɡ���� ![]() ���ӣ���֪������ʱ�䲻����
���ӣ���֪������ʱ�䲻���� ![]() Сʱ��������һ�������ɻ�����
Сʱ��������һ�������ɻ����� ![]() Ԫ������һ������ɻ�����
Ԫ������һ������ɻ����� ![]() Ԫ������һ��ɡ���ɻ�����
Ԫ������һ��ɡ���ɻ����� ![]() Ԫ.
Ԫ.
��1����ÿ���������������� ![]() ���������
��������� ![]() ��ʾÿ�������
��ʾÿ������� ![]() ��Ԫ����
��Ԫ����
��2����ô���������������ʹÿ������������������Ƕ��٣�
���𰸡�
��1���⣺������ÿ��������ɡ������Ϊ100��x��y��
��������w��5x��6y��3��100��x��y����2x��3y��300
��2���⣺Լ������Ϊ 
������ 
Ŀ�꺯��Ϊw��2x��3y��300.
������������ͼ��ʾ��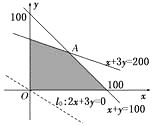
��ʼֱ��l0��2x��3y��0��ƽ�Ƴ�ʼֱ�߾�����Aʱ��w�����ֵ��
�� ![]() ��
�� ![]()
���Ž�ΪA��50,50��������wmax��550Ԫ��
����ÿ����������50�������50����ɡ��0��ʱ��������Ϊ����550Ԫ
��������������Ŀ���������������ص㣬������������x�����������y����������ɡ����100-x-y��������������Ϊz=5x+6y+3��100-x-y��=2x+3y+300����������ʱ����������������г�Լ������������ƽ�����������Թ滮֪ʶ������Ž⣮�����˼����Թ滮��Ӧ�ã��г�Լ���������ó�Ŀ�꺯���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �Ľ�
�Ľ�![]() ���Եı߷ݱ�Ϊ
���Եı߷ݱ�Ϊ![]() ����
����![]()
��1�����![]() �Ĵ�С��
�Ĵ�С��
��2����![]() ����
����![]() ���ܳ�
���ܳ�![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������![]() ��,����
��,����![]() ��������,
��������, ![]() ��
��![]() ���ڵ�
���ڵ�![]() ,
,![]() ����
����![]() ,
,![]() Ϊ
Ϊ![]() ���е�.
���е�.
(1).��֤: ![]() ƽ��
ƽ��![]() ;
;
(2).��֤: ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
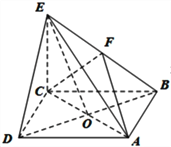
����Ŀ����ͼ����֪������ABCD�;���ACEF����ƽ�����ֱ��AB= ![]() ��AF=1��GΪ�߶�AD�ϵ�����һ�㣮
��AF=1��GΪ�߶�AD�ϵ�����һ�㣮 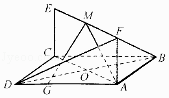
��1����M���߶�EF���е㣬֤����ƽ��AMG��ƽ��BDF��
��2����NΪ�߶�EF������һ�㣬��ֱ��AN��ƽ��ABF��ƽ��BDF���ɽǷֱ��Ǧ����£��� ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ͧ���쳧�з���һ������ͧ������ǰ5���µIJ������£�

��1����![]() ����
����![]() �Ļع�ֱ�߷���Ϊ
�Ļع�ֱ�߷���Ϊ![]() �ָ��ݱ��������Ѿ���ȷ�������
�ָ��ݱ��������Ѿ���ȷ�������![]() ��ֵΪ
��ֵΪ![]() ������
������![]() ��ֵ�������Ƹó�
��ֵ�������Ƹó�![]() �·ݵIJ���������������ȷ��
�·ݵIJ���������������ȷ��![]() ��
��
�����ʼ첿�ŷ��ָó�![]() �·���������ͧ�������������⣬Ҫ���ٻأ�����һ���ι�˾����ó������˽���ǰ��������������ͧ
�·���������ͧ�������������⣬Ҫ���ٻأ�����һ���ι�˾����ó������˽���ǰ��������������ͧ![]() �ң�������ι�˾����ͧ���ٻصĸ���.
�ң�������ι�˾����ͧ���ٻصĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڰ뾶ΪR��Բ�ڣ����ڽӵ�����ABC�����ױ��ϸ�h�ʣ�0��t]ʱ����ABC�����ȡ�����ֵ ![]() ����t��ȡֵ��Χ�� ��
����t��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ ![]() �У�����Բ
�У�����Բ ![]()
![]() ��������������ֱ�Ϊ
��������������ֱ�Ϊ ![]() �����ҽ���
�����ҽ��� ![]() ����
���� ![]() �ᴹֱ��ֱ��
�ᴹֱ��ֱ�� ![]() ����Բ
����Բ ![]() �ཻ������һ������Ϊ
�ཻ������һ������Ϊ ![]() .
.
��1������Բ ![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() .
.
��1��![]() ʱ��֤����
ʱ��֤���� ![]() ��
��
��2���� ![]() ʱ��ֱ��
ʱ��ֱ�� ![]() ������
������ ![]() ���ڵ�
���ڵ� ![]() ����ʵ��
����ʵ�� ![]() ��ֵ��
��ֵ��
��3���� ![]() ʱ������ʽ
ʱ������ʽ ![]() ���������ʵ��
���������ʵ�� ![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������³����ͼ����������t��[0��5]�������S���ڣ� �� 
A.[��4��10��
B.[��5��2]
C.[��4��3]
D.[��2��5]
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com