
【题目】已知函数f(x)=4x2﹣4ax+a2﹣2a+2在区间[0,2]上有最小值3,求实数a的值.
【答案】![]() 或
或![]()
【解析】试题分析:确定二次函数的最值,首先要确定其在定义域上的单调性,本题中二次函数对称轴为![]() ,因此首先讨论对称轴位置的三种情况:
,因此首先讨论对称轴位置的三种情况:![]() ≤0,0<
≤0,0<![]() <2,
<2,![]() ≥2,从而确定其单调性,将最值转化为用a表示的关系式,求解a值
≥2,从而确定其单调性,将最值转化为用a表示的关系式,求解a值
试题解析:∵f(x)=4(x-![]() )2-2a+2,
)2-2a+2,
①当![]() ≤0,即a≤0时,函数f(x)在[0,2]上是增函数.
≤0,即a≤0时,函数f(x)在[0,2]上是增函数.
∴f(x)min=f(0)=a2-2a+2.
由a2-2a+2=3,得a=1±![]() .
.
∵a≤0,∴a=1-![]() .
.
②当0<![]() <2,即0<a<4时,
<2,即0<a<4时,
f(x)min=f(![]() )=-2a+2.
)=-2a+2.
由-2a+2=3,得a=-![]() (0,4),舍去.
(0,4),舍去.
③当![]() ≥2,即a≥4时,函数f(x)在[0,2]上是减函数,
≥2,即a≥4时,函数f(x)在[0,2]上是减函数,
f(x)min=f(2)=a2-10a+18.
由a2-10a+18=3,得a=5±![]() .
.
∵a≥4,∴a=5+![]() .
.
综上所述,a=1-![]() 或a=5+
或a=5+![]() .
.


科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出![]() 与销售额
与销售额![]() (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求回归直线方程;
(2)试预测广告费支出为![]() 万元时,销售额多大?
万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过![]() 的概率.(参考数据:
的概率.(参考数据: 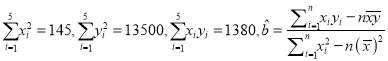 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一鲜花店一个月(30天)某种鲜花的日销售量与销售天数统计如下:
日销售量(枝) | 0~49 | 50~99 | 100~149 | 150~199 | 200~250 |
销售天数(天) | 3天 | 3天 | 15天 | 6天 | 3天 |
将日销售量落入各组区间的频率视为概率.
(1)试求这30天中日销售量低于100枝的概率;
(2)若此花店在日销售量低于100枝的6天中选择2天作促销活动,求这2天的日销售量都低于50枝的概率(不需要枚举基本事件).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 越大,说明“
越大,说明“![]() 与
与![]() 有关系”的可信度越大.
有关系”的可信度越大.
②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() 的值分别是
的值分别是![]() 和0.3.
和0.3.
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为![]() 中,
中, ![]() ,
,
则![]() .正确的个数是( )
.正确的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数对![]() 一切实数
一切实数![]() 都有
都有![]() ,且当
,且当![]() 时,
时,![]() ,又
,又![]() .
.
(1)判断该函数的奇偶性并说明理由;、
(2)试判断该函数在![]() 上的单调性;
上的单调性;
(3)求![]() 在区间
在区间![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长均相等的正三棱柱ABCA1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:
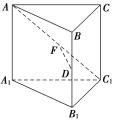
①AC1⊥BC;
②AF=FC1;
③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
A.0 B.1
C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2-a≤x≤2+a},B={x|x≤1或x≥4}.
(1)当a=3时,求A∩B;
(2)若a>0,且A∩B=![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com