
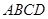 中,
中,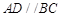 ,
,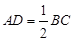 ,
,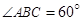 ,
,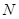 是
是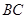 的中点.将梯形
的中点.将梯形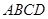 绕
绕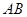 旋转
旋转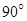 ,得到梯形
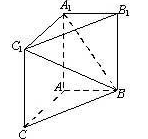
,得到梯形 (如图).
(如图).
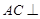 平面
平面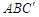 ;
; 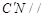 平面
平面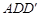 ;
;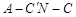 的余弦值.
的余弦值.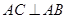 由已知可知 平面
由已知可知 平面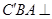 平面
平面 ,结合面面垂直的性质定理得到.
,结合面面垂直的性质定理得到.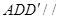 平面
平面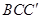 ,又因为
,又因为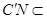 平面
平面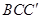 ,所以
,所以 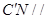 平面
平面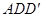 从而得到证明.
从而得到证明.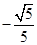
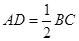 ,
,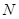 是
是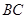 的中点
的中点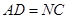 ,又
,又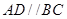
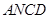 是平行四边形,所以
是平行四边形,所以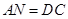
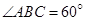 ,
,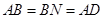 ,所以四边形
,所以四边形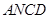 是菱形,所以
是菱形,所以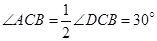
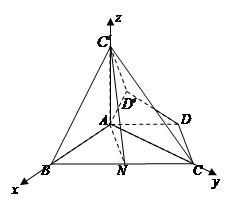
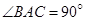 ,即
,即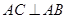
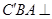 平面
平面 ,
,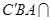 平面
平面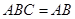
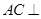 平面
平面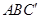 4分
4分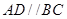 ,
,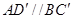 ,
, 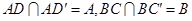
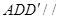 平面
平面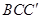
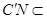 平面
平面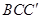 ,所以
,所以 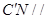 平面
平面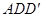 8分
8分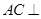 平面
平面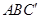 ,同理
,同理 平面
平面 ,建立如图如示坐标系
,建立如图如示坐标系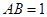 ,
,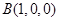 ,
, ,
, 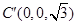 ,
,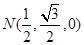 , 9分
, 9分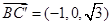 ,
,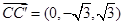
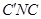 的法向量为
的法向量为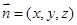 ,有
,有 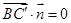 ,
,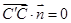 得
得 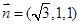
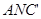 的法向量为
的法向量为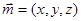 ,有
,有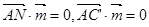

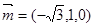 12分
12分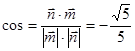 13分
13分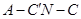 为钝角
为钝角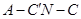 的余弦值为
的余弦值为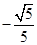 . 14分
. 14分

科目:高中数学 来源:不详 题型:解答题
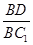 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.垂直和平行 | B.均为平行 | C.均为垂直 | D.不确定 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
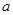 、
、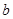 、
、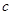 表示三条不同的直线,
表示三条不同的直线,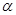 表示平面,给出下列命题:
表示平面,给出下列命题: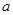 ∥
∥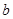 ,
,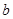 ∥
∥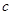 ,则
,则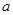 ∥
∥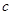 ; ②若
; ②若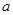 ⊥
⊥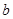 ,
,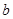 ⊥
⊥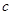 ,则
,则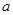 ⊥
⊥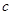 ;
;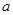 ∥
∥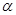 ,
,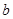 ∥
∥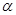 ,则
,则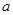 ∥
∥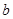 ; ④若
; ④若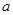 ⊥
⊥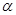 ,
,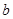 ⊥
⊥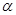 ,则
,则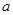 ∥
∥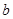 .
.| A.①② | B.②③ | C.①④ | D.③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com