
【题目】已知函数f(x)= ![]() e﹣ax(a>0).
e﹣ax(a>0).
(1)当a=2时,求曲线y=f(x)在x= ![]() 处的切线方程;
处的切线方程;
(2)讨论方程f(x)﹣1=0根的个数.
【答案】
(1)解:当a=2时,f(x)= ![]() e﹣2x.f(
e﹣2x.f( ![]() )=3e﹣1,
)=3e﹣1,
又f′(x)= ![]() e﹣2x,∴f′(
e﹣2x,∴f′( ![]() )=2e﹣1,
)=2e﹣1,
故所求切线方程为y﹣3e﹣1=2e﹣1(x﹣ ![]() ),即y=
),即y= ![]() x+
x+ ![]()
(2)解:方程f(x)﹣1=0即f(x)=1.
f(x)的定义域为(﹣∞,1)∪(1,+∞),
当x<﹣1或x>1时,易知f(x)<0,故方程f(x)=1无解;
故只需考虑﹣1≤x≤1的情况,
f′(x)= ![]() e﹣2x,
e﹣2x,
当<a≤2时,f′(x)≥0,所以f(x)区间[﹣1,1)上是增函数,又易知f(0)=1,
所以方程f(x)=1只有一个根0;
当a>2时,由f′(x)=0可得x=± ![]() ,且0<
,且0< ![]() <1,
<1,
由f′(x)>0可得﹣1≤x<﹣ ![]() 或
或 ![]() <x<1,
<x<1,
由f′(x)<0可得﹣ ![]() <x<
<x< ![]() ,
,
所以f(x)单调增区间为[﹣1,﹣ ![]() )和(
)和( ![]() ,1)上是增函数,
,1)上是增函数,
f(x)单调减区间为(﹣ ![]() ,
, ![]() ),
),
由上可知f( ![]() )<f(0)<f(﹣
)<f(0)<f(﹣ ![]() ),即f(
),即f( ![]() )<1<f(﹣
)<1<f(﹣ ![]() ),
),
在区间(﹣ ![]() ,
, ![]() span> )上f(x)单调递减,且f(0)=1,
span> )上f(x)单调递减,且f(0)=1,
所以方程f(x)=1有唯一的根x=0;
在 区间[﹣1,﹣ ![]() )上f(x)单调递增,且f(﹣1)=0<1,f(﹣
)上f(x)单调递增,且f(﹣1)=0<1,f(﹣ ![]() )>1,
)>1,
所以方程f(x)=1存在唯一的根0
在区间( ![]() ,1)上,由f(
,1)上,由f( ![]() )<1,x→1时,f(x)→+∞,
)<1,x→1时,f(x)→+∞,
所以方程f(x)=1有唯一的根;
综上所述:当0<a≤2时,方程f(x)=1有1个根;
当a>2时,方程f(x)=1有3个根
【解析】(1)当a=2时,求函数的导数,利用导数的几何意义进行求解即可.(2)由f(x)﹣1=0得f(x)=1,求函数的导数f′(x),判断函数的单调性,利用函数单调性和最值之间的关系进行判断即可.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某同学在用120分钟做150分的数学试卷(分为卷Ⅰ和卷Ⅱ两部分)时,卷Ⅰ和卷Ⅱ所得分数分别为P(单位:分)和Q(单位:分),在每部分做了20分钟的条件下发现它们与投入时间m(单位:分钟)的关系有经验公式,![]() .
.
(1)试建立数学总成绩y(单位:分)与对卷Ⅱ投入时间x(单位:分钟)的函数关系式,并指明函数定义域;
(2)如何计划使用时间,才能使得所得分数最高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 交此抛物线于不同的两个点
交此抛物线于不同的两个点![]() 、
、![]() .
.
(![]() )当直线
)当直线![]() 过点
过点![]() 时,证明
时,证明![]() ,
,![]() 为定值.
为定值.
(![]() )当
)当![]() 时,直线
时,直线![]() 是否过定点?若过定点,求出定点坐标;反之,请说明理由.
是否过定点?若过定点,求出定点坐标;反之,请说明理由.
(![]() )记
)记![]() ,如果直线
,如果直线![]() 过点
过点![]() ,设线段
,设线段![]() 的中点为
的中点为![]() ,线段
,线段![]() 的中点为
的中点为![]() .问是否存在一条直线和一个定点,使得点
.问是否存在一条直线和一个定点,使得点![]() 到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.
到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与
与![]() 轴负半轴相交于点
轴负半轴相交于点![]() ,与
,与![]() 轴正半轴相交于点
轴正半轴相交于点![]() .
.
(1)若过点 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若在以![]() 为圆心半径为
为圆心半径为![]() 的圆上存在点
的圆上存在点![]() ,使得
,使得![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围;
的取值范围;
(3)设![]() 是圆
是圆![]() 上的两个动点,点
上的两个动点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,如果直线
,如果直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 和
和![]() ,问
,问![]() 是否为定值?若是求出该定值;若不是,请说明理由.
是否为定值?若是求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于n∈N* , 若数列{xn}满足xn+1﹣xn>1,则称这个数列为“K数列”.
(Ⅰ)已知数列:1,m+1,m2是“K数列”,求实数m的取值范围;
(Ⅱ)是否存在首项为﹣1的等差数列{an}为“K数列”,且其前n项和Sn满足 ![]() ?若存在,求出{an}的通项公式;若不存在,请说明理由;
?若存在,求出{an}的通项公式;若不存在,请说明理由;
(Ⅲ)已知各项均为正整数的等比数列{an}是“K数列”,数列 ![]() 不是“K数列”,若
不是“K数列”,若 ![]() ,试判断数列{bn}是否为“K数列”,并说明理由.
,试判断数列{bn}是否为“K数列”,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
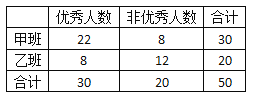
【题目】教育学家分析发现加强语文乐队理解训练与提高数学应用题得分率有关,某校兴趣小组为了验证这个结论,从该校选择甲乙两个同轨班级进行试验,其中甲班加强阅读理解训练,乙班常规教学无额外训练,一段时间后进行数学应用题测试,统计数据情况如下面的![]() 列联表(单位:人)
列联表(单位:人)
(1)经过多次测试后,小明正确解答一道数学应用题所用的时
间在5—7分钟,小刚正确解得一道数学应用题所用的时间在6—8
分钟,现小明.小刚同时独立解答同一道数学应用题,求小刚比
小明先正确解答完的概率;
(2)现从乙班成绩优秀的8名同学中任意抽取两人,并对他们的答题情况进行全程研究,记A.B两人中被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在
,若存在![]() 成立,则称
成立,则称![]() 的不动点.如果函数
的不动点.如果函数
![]() 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且![]()
(1)求函数![]() 的解析式;
的解析式;
(2)已知各项不为零的数列![]() ,求数列通项
,求数列通项![]() ;
;
(3)如果数列![]() 满足
满足![]() ,求证:当
,求证:当![]() 时,恒有
时,恒有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起.设折起后点
折起.设折起后点![]() 的位置为
的位置为![]() ,并且平面
,并且平面![]()
![]() 平面
平面![]() .给出下面四个命题:
.给出下面四个命题:
①![]() ;②三棱锥
;②三棱锥![]() 的体积为
的体积为![]() ;③
;③![]()
![]() 平面
平面![]() ;
;
④平面![]() 平面
平面![]() .其中正确命题的序号是( )
.其中正确命题的序号是( )


A. ①② B. ③④ C. ①③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在汶川大地震后对唐家山堰塞湖的抢险过程中,武警官兵准备用射击的方法引爆从湖坝上游漂流而下的一个巨大的汽油罐.已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆.每次射击是相互独立的,且命中的概率都是 ![]() .
.
(Ⅰ)求油罐被引爆的概率;
(Ⅱ)如果引爆或子弹打光则停止射击,设射击次数为ξ.求ξ的分布列及数学期望E(ξ).( 结果用分数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com