解:(Ⅰ)∵函数f(x)=x
2+bx+c为偶函数
∴f(-x)=f(x)
∴x
2-bx+c=x
2+bx+c
∴b=0
∵函数f(x)=x
2+bx+c(常数b、c∈R)的一个零点为1,
∴f(1)=0
∴c=-1
∴函数y=f(x)的解析式为f(x)=x
2-1;
(Ⅱ)直线l:y=kx+m代入y=x
2-1,∴x
2-kx-m-1=0
∵直线l:y=kx+m(k>m∈R)与函数y=f(x)的图象相切
∴△=k
2-4(-m-1)=k
2+4m+4=0
∴

∴
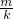
=

∵k>0,∴
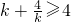
∴
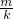
=

≤-1
∴
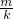
的取值范围是(-∞,-1]
分析:(Ⅰ)根据函数f(x)=x
2+bx+c为偶函数,可得b=0,根据函数f(x)=x
2+bx+c(常数b、c∈R)的一个零点为1,可得c=-1,从而可求函数y=f(x)的解析式;
(Ⅱ)直线l:y=kx+m代入y=x
2-1,利用直线l:y=kx+m(k>m∈R)与函数y=f(x)的图象相切,可判别式为0,从而

,进而可得
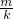
=

,利用基本不等式可求
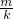
的取值范围.
点评:本题重点考查函数的解析式,考查直线与函数图象的位置关系,考查基本不等式的运用,综合性强.

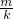 的取值范围.
的取值范围.
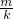 =
=
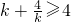
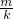 =
= ≤-1
≤-1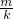 的取值范围是(-∞,-1]
的取值范围是(-∞,-1] ,进而可得
,进而可得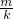 =
= ,利用基本不等式可求
,利用基本不等式可求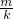 的取值范围.
的取值范围.
