练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数是定义在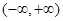上的奇函数，且.
    （1）求实数的值.（2）用定义证明在上是增函数；
    （3）写出的单调减区间，并判断有无最大值或最小值？如有，写出最大值或最小值（无需说明理由）
    （1）∵是奇函数，∴
    ∴    ∴---------------3分
    故 又　∵， ∴　　   --------5分
    ∴　  -----------------------6分
    （2）任取，

    ∵ ∴，，，
    ，  ∴即
    ∴在上是增函数.                       ----------10分
    (3)单调减区间为；
    当时，；当时，.
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    已知函数的图象（部分）如图所示，则的解析式是
    A．
    B．
    C．
    D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    某校要建造一个容积为8，深为2的长方体无盖水池，池底和池壁的造价每平方米分别为240元和160元，那么水池的最低总造价为               元。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知定义域为的单调函数满足：对任意均成立.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知且，若，则的取值范围是（   ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    函数在区间上是减函数，则实数的取值范围(　)
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    方程的实数根的个数为（   ）
    A．0B．1C．2D．不确定

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

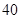    某商品进货单价为元，若销售价为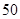元，可卖出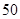个，如果销售单价每涨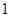元，销售量就减少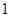个，为了获得最大利润，则此商品的最佳售价应为_________

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某种出口产品的关税税率t．市场价格x(单位：千元)与市场供应量p(单位：万件)之间近似满足关系式：，其中k．b均为常数．当关税税率为75%时，若市场价格为5千元，则市场供应量约为1万件；若市场价格为7千元，则市场供应量约为2万件．
    (1)试确定k．b的值；
    (2)市场需求量q(单位：万件)与市场价格x近似满足关系式：．P = q时，市场价格称为市场平衡价格．当市场平衡价格不超过4千元时，试确定关税税率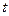的最大值．

    查看答案和解析>>

    同步练习册答案