
【题目】如图,三棱锥![]() 的三个侧面均为边长是
的三个侧面均为边长是![]() 的等边三角形,
的等边三角形, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
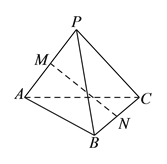
(I)求![]() 的长.
的长.
(II)求证: ![]() .
.
(III)求三棱锥![]() 的表面积.
的表面积.
科目:高中数学 来源: 题型:
【题目】.某几何体如图所示, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是边长为
是边长为![]() 的正三角形,
的正三角形, ![]() ,
, ![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
(I)求证: ![]() 平面
平面![]() .
.
(II)求证:平面![]() 平面
平面![]() .
.
(III)求该几何体的体积.
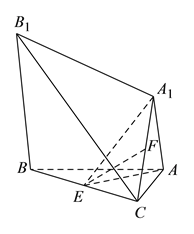
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体![]() 的棱长为
的棱长为![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,过直线
的中点,过直线![]() ,
,![]() 的平面分别与棱
的平面分别与棱![]() 、
、![]() 交于
交于![]() ,
,![]() ,设
,设![]() ,
,![]() ,给出以下四个命题:
,给出以下四个命题:
①平面![]() 平面
平面![]() ;
;
②当且仅当![]() 时,四边形
时,四边形![]() 的面积最小;
的面积最小;
③四边形![]() 周长
周长![]() ,
,![]() 是单调函数;
是单调函数;
④四棱锥![]() 的体积
的体积![]() 为常函数;
为常函数;
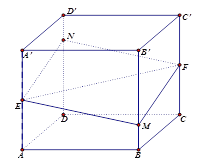
以上命题中假命题的序号为( ).
A. ①④ B. ② C. ③ D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥S﹣ABC中,SA⊥AB,SA⊥AC,AC⊥BC且AC=2,BC=![]() , SB=
, SB=![]() .
.
(1)证明:SC⊥BC;
(2)求三棱锥的体积VS﹣ABC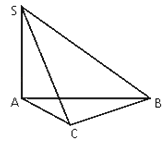
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t≤1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如表:
分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
(1)画出频率分布表,并画出频率分布直方图;
(2)估计纤度落在![]() 中的概率及纤度小于
中的概率及纤度小于![]() 的概率是多少?
的概率是多少?
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为![]() 。
。
(1)求乙投球的命中率![]() 。
。
(2)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com