
【题目】某市环保部门对市中心每天的环境污染情况进行调查研究后,发现一天中环境综合污染指数![]() 与时刻
与时刻![]() (时)的关系为
(时)的关系为![]() ,
,![]() ,其中
,其中![]() 是与气象有关的参数,且
是与气象有关的参数,且![]() .若用每天
.若用每天![]() 的最大值为当天的综合污染指数,并记作
的最大值为当天的综合污染指数,并记作![]() .
.
(1)令![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)求![]() 的表达式,并规定当
的表达式,并规定当![]() 时为综合污染指数不超标,求当
时为综合污染指数不超标,求当![]() 在什么范围内时,该市市中心的综合污染指数不超标.
在什么范围内时,该市市中心的综合污染指数不超标.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】已知四棱台![]() 的上下底面分别是边长为2和4的正方形,
的上下底面分别是边长为2和4的正方形, ![]() = 4且
= 4且 ![]() ⊥底面
⊥底面![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
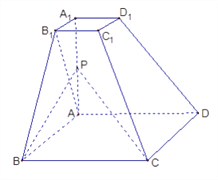
(Ⅰ)求证: ![]() 面
面 ![]() ;
;
(Ⅱ)在![]() 边上找一点
边上找一点![]() ,使
,使![]() ∥面
∥面![]() ,
,
并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的上顶点为
)的上顶点为![]() ,左焦点为
,左焦点为![]() ,离心率为
,离心率为![]() ,直线
,直线![]() 与圆
与圆![]() 相切.
相切.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 且斜率存在的直线
且斜率存在的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,线段
两点,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,试判断
,试判断![]() 是否为定值?并说明理由.
是否为定值?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1 000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1 200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
W | 12 | 15 | 18 |
P | 0.3 | 0.5 | 0.2 |
该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.
(I)求Z的分布列和均值;
(II)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10 000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“伟大的变革—庆祝改革开放40周年大型展览”于2019年3月20日在中国国家博物馆闭幕,本次特展紧扣“改革开放40年光辉历程”的主线,多角度、全景式描绘了我国改革开放40年波澜壮阔的历史画卷.据统计,展览全程呈现出持续火爆的状态,现场观众累计达423万人次,参展人数屡次创造国家博物馆参观纪录,网上展馆点击浏览总量达4.03亿次.
下表是2019年2月参观人数(单位:万人)统计表
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
人数 | 3.0 | 3.1 | 2.5 | 2.3 | 5.4 | 6.8 | 6.2 | 6.7 | 5.5 | 4.9 | 3.2 | 3.0 | 2.7 | 2.5 |
日期 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
人数 | 2.4 | 2.9 | 3.2 | 2.8 | 2.9 | 2.3 | 3.0 | 2.9 | 3.1 | 3.0 | 3.1 | 3.1 | 3.1 | 3.0 |
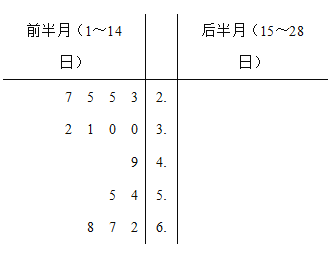
根据表中数据回答下列问题:
(1)请将2019年2月前半月(1~14日)和后半月(15~28日)参观人数统计对比茎叶图填补完整,并通过茎叶图比较两组数据方差的大小(不要求计算出具体值,得出结论即可);
(2)将2019年2月参观人数数据用该天的对应日期作为样本编号,现从中抽样7天的样本数据.若抽取的样本编号是以4为公差的等差数列,且数列的第4项为15,求抽出的这7个样本数据的平均值;
(3)根据国博以往展览数据及调查统计信息可知,单日入馆参观人数为0~3(含3,单位:万人)时,参观者的体验满意度最佳,在从(2)中抽出的样本数据中随机抽取两天的数据,求这两天参观者的体验满意度均为最住的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左焦点为
)的左焦点为![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() 与
与![]() 轴垂直,
轴垂直,![]() ,
,![]() 分别为椭圆的右顶点和上顶点,且
分别为椭圆的右顶点和上顶点,且![]() ,且
,且![]() 的面积是
的面积是![]() ,其中
,其中![]() 是坐标原点.
是坐标原点.
(1)求椭圆![]() 的方程.
的方程.
(2)若过点![]() 的直线
的直线![]() ,
,![]() 互相垂直,且分别与椭圆
互相垂直,且分别与椭圆![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() 四点,求四边形
四点,求四边形![]() 的面积
的面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知四边形
中,已知四边形![]() 是边长为
是边长为![]() 的正方形,点
的正方形,点![]() 是
是![]() 的中点,点
的中点,点![]() 在底面
在底面![]() 上的射影为点
上的射影为点![]() ,点
,点![]() 在棱
在棱![]() 上,且四棱锥
上,且四棱锥![]() 的体积为
的体积为![]() .
.
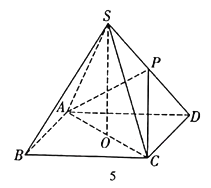
(1)若点![]() 是
是![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com