
【题目】已知直线![]() :
: ![]() ,圆
,圆![]() :
: ![]()
(1)求证:直线![]() 与圆
与圆![]() 总相交;
总相交;
(2)求出相交的弦长的最小值及相应的![]() 值;
值;
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】阅读与探究
人教A版《普通高中课程标准实验教科书 数学4(必修)》在第一章的小结中写到:
将角放在直角坐标系中讨论不但使角的表示有了统一的方法,而且使我们能够借助直角坐标系中的单位圆,建立角的变化与单位圆上点的变化之间的对应关系,从而用单位圆上点的纵坐标、横坐标来表示圆心角的正弦函数、余弦函数.因此,正弦函数、余弦函数的基本性质与圆的几何性质(主要是对称性)之间存在着非常紧密的联系.例如,和单位圆相关的“勾股定理”与同角三角函数的基本关系有内在的一致性;单位圆周长为![]() 与正弦函数、余弦函数的周期为
与正弦函数、余弦函数的周期为![]() 是一致的;圆的各种对称性与三角函数的奇偶性、诱导公式等也是一致的等等.因此,三角函数的研究过程能够很好地体现数形结合思想.
是一致的;圆的各种对称性与三角函数的奇偶性、诱导公式等也是一致的等等.因此,三角函数的研究过程能够很好地体现数形结合思想.
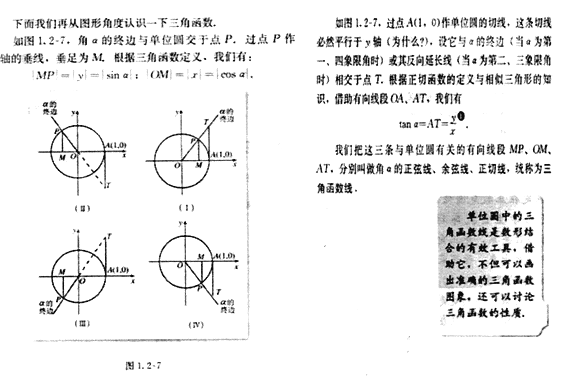
依据上述材料,利用正切线可以讨论研究得出正切函数![]() 的性质.
的性质.
比如:由图1.2-7可知,角![]() 的终边落在四个象限时均存在正切线;角
的终边落在四个象限时均存在正切线;角![]() 的终边落在
的终边落在![]() 轴上时,其正切线缩为一个点,值为
轴上时,其正切线缩为一个点,值为![]() ;角
;角![]() 的终边落在
的终边落在![]() 轴上时,其正切线不存在;所以正切函数
轴上时,其正切线不存在;所以正切函数![]() 的定义域是
的定义域是![]() .
.
(1)请利用单位圆中的正切线研究得出正切函数![]() 的单调性和奇偶性;
的单调性和奇偶性;
(2)根据阅读材料中途1.2-7,若角![]() 为锐角,求证:
为锐角,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点(0,1)的直线与圆x2+y2=4相交于A、B两点,若 ![]() ,则点P的轨迹方程是( )
,则点P的轨迹方程是( )
A.![]()
B.x2+(y﹣1)2=1
C.![]()
D.x2+(y﹣1)2=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
. ![]() 在
在![]() 上有最大值9,最小值4.
上有最大值9,最小值4.
(1)求实数![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若方程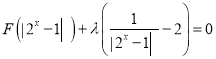 有三个不同的实数根,求实数
有三个不同的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A是抛物线M:y2=2px(p>0)与圆C:x2+(y﹣4)2=a2在第一象限的公共点,且点A到抛物线M焦点F的距离为a,若抛物线M上一动点到其准线与到点C的距离之和的最小值为2a,O为坐标原点,则直线OA被圆C所截得的弦长为( )
A.2
B.2 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“a=﹣1”是“直线ax+3y+2=0与直线x+(a﹣2)y+1=0平行”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com