
【题目】如图,圆C与x轴相切于点T(2,0),与y轴的正半轴相交于A,B两点(A在B的上方),且AB=3.

(1)求圆C的方程;
(2)直线BT上是否存在点P满足PA2+PB2+PT2=12,若存在,求出点P的坐标,若不存在,请说明理由;
(3)如果圆C上存在E,F两点,使得射线AB平分∠EAF,求证:直线EF的斜率为定值.
【答案】(1)![]() ;(2)点P坐标为
;(2)点P坐标为![]() .(3)见解析.
.(3)见解析.
【解析】
(1)求出圆C的半径为![]() ,即得圆C的方程;(2)先求出直线BT的方程为x+2y-2=0.
,即得圆C的方程;(2)先求出直线BT的方程为x+2y-2=0.
设P(2-2y,y),根据PA2+PB2+PT2=12 求出点P的坐标;(3)由题得![]() ,即EF⊥BC,再求EF的斜率.
,即EF⊥BC,再求EF的斜率.
(1)由题得![]() ,所以圆C的半径为
,所以圆C的半径为![]() .
.
所以圆C的方程为![]() .
.
(2)在![]() 中,令x=0,则y=1或y=4.
中,令x=0,则y=1或y=4.
所以A(0,4),B(0,1).
所以直线BT的方程为x+2y-2=0.
设P(2-2y,y),因为PA2+PB2+PT2=12,
所以![]() ,
,
由题得![]()
因为![]() ,
,
所以方程无解.
所以不存在这样的点P.
(3)由题得![]() ,
,
所以 ,
,
所以![]() .
.
所以直线EF的斜率为定值.


科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PB=PD=2,PA= ![]() .
. 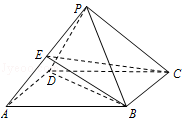
(Ⅰ)求证:BD⊥PC;
(Ⅱ)若E是PA的中点,求三棱锥P﹣BCE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了140位市民进行调查,调查结果统计如下:
支持 | 不支持 | 总计 | |
男性市民 | 60 | ||
女性市民 | 50 | ||
合计 | 70 | 140 |
(I)根据已知数据,把表格数据填写完整;
(II)利用(1)完成的表格数据回答下列问题:
(ⅰ)能否在犯错误的概率不超过0.001的前提下认为性别与支持申办足球世界杯有关;
(ⅱ)已知在被调查的支持申办足球世界杯的男性市民中有5位退休老人,其中2位是教师,现从这5位退休老人中随机抽取3人,求至多有1位老师的概率。
附:![]() ,其中
,其中![]()
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , O为坐标原点,点P(1,
=1(a>b>0)的左、右焦点分别为F1 , F2 , O为坐标原点,点P(1, ![]() )在椭圆上,连接PF1交y轴于点Q,点Q满足
)在椭圆上,连接PF1交y轴于点Q,点Q满足 ![]() =
= ![]() .直线l不过原点O且不平行于坐标轴,l与椭圆C有两个交点A,B. (Ⅰ)求椭圆C的标准方程;
.直线l不过原点O且不平行于坐标轴,l与椭圆C有两个交点A,B. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知点M( ![]() ,0),若直线l过椭圆C的右焦点F2 , 证明:
,0),若直线l过椭圆C的右焦点F2 , 证明: ![]()
![]() 为定值;
为定值;
(Ⅲ)若直线l过点(0,2),设N为椭圆C上一点,且满足 ![]() +
+ ![]() =λ
=λ ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两名篮球运动员分别在各自不同的5场比赛所得篮板球数的茎叶图如图所示,已知两名运动员在各自5场比赛所得平均篮板球数均为10.
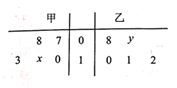
(1)求x,y的值;
(2)求甲乙所得篮板球数的方差![]() 和
和![]() ,并指出哪位运动员篮板球水平更稳定;
,并指出哪位运动员篮板球水平更稳定;
(3)教练员要对甲乙两名运动员篮板球的整体水平进行评估.现在甲乙各自的5场比赛中各选一场进行评估,则两名运动员所得篮板球之和小于18的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数f(x)是定义在R上的偶函数,f(x+1)为奇函数,f(0)=0,当x∈(0,1]时,f(x)=log2x,则在区间(8,9)内满足方f(x)程f(x)+2=f( ![]() )的实数x为( )
)的实数x为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AB⊥平面BB1C1C,∠BCC1= ![]() ,AB=BB1=2,BC=1,D为CC1中点.
,AB=BB1=2,BC=1,D为CC1中点. 
(1)求证:DB1⊥平面ABD;
(2)求二面角A﹣B1D﹣A1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足 ![]() ,
, ![]() ,其中n∈N+ . (I)求证:数列{bn}是等差数列,并求出数列{an}的通项公式;
,其中n∈N+ . (I)求证:数列{bn}是等差数列,并求出数列{an}的通项公式;
(II)设 ![]() ,求数列{cncn+2}的前n项和为Tn .
,求数列{cncn+2}的前n项和为Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在底面为正方形的四棱锥S﹣ABCD中,SA=SB=SC=SD,异面直线AD与SC所成的角为60°,AB=2.则四棱锥S﹣ABCD的外接球的表面积为( ) 
A.6π
B.8π
C.12π
D.16π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com