
分析 (1)由曲线C1:x+y=4可得曲线C1的极坐标方程;先将曲线C2化为普通方程,进而可得曲线C2的极坐标方程;
(2)设A(ρ1,α),B(ρ2,α),-$\frac{π}{4}$<α<$\frac{π}{2}$,则ρ1=$\frac{4}{cosα+sinα}$,ρ2=2cosα,则$\frac{|OB|}{|OA|}$=$\frac{ρ2}{ρ1}$,进而得到答案.
解答 解:(1)∵在直角坐标系xOy中,曲线C1:x+y=4,
曲线C1的极坐标方程为:ρ(cosθ+sinθ)=4,
C2的普通方程为(x-1)2+y2=1,
所以曲线C2的极坐标方程为:ρ=2cosθ.…(4分)
(2)设A(ρ1,α),B(ρ2,α),-$\frac{π}{4}$<α<$\frac{π}{2}$,
则ρ1=$\frac{4}{cosα+sinα}$,ρ2=2cosα,…(6分)
$\frac{|OB|}{|OA|}$=$\frac{ρ2}{ρ1}$=$\frac{1}{4}$×2cosα(cosα+sinα)
=$\frac{1}{4}$(cos2α+sin2α+1)=$\frac{1}{4}$[$\sqrt{2}$cos(2α-$\frac{π}{4}$)+1],…(8分)
当α=$\frac{π}{8}$时,$\frac{|OB|}{|OA|}$取得最大值$\frac{1}{4}$($\sqrt{2}$+1).…(10分)
点评 本题考查的知识点是直线与圆的极坐标方程,圆的参数方程,三角函数的最值,难度中档.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 672 | B. | 673 | C. | 3024 | D. | 1345 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
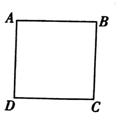 如图,正方形ABCD边长为1,从某时刻起,将线段AB,BC,CD,DA分别绕点A,B,C,D顺时针旋转相同角度α(0<α<$\frac{π}{2}$),若旋转后的四条线段所围成的封闭图形面积为$\frac{1}{2}$,则α=( )
如图,正方形ABCD边长为1,从某时刻起,将线段AB,BC,CD,DA分别绕点A,B,C,D顺时针旋转相同角度α(0<α<$\frac{π}{2}$),若旋转后的四条线段所围成的封闭图形面积为$\frac{1}{2}$,则α=( )| A. | $\frac{π}{12}$或$\frac{5π}{12}$ | B. | $\frac{π}{12}$或$\frac{π}{3}$ | C. | $\frac{π}{6}$或$\frac{5π}{12}$ | D. | $\frac{π}{6}$或$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
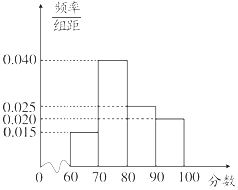 2016年年底,某商业集团根据相关评分标准,对所属20家商业连锁店进行了年度考核评估,并依据考核评估得分(最低分60分,最高分100分)将这些连锁店分别评定为A,B,C,D四个类型,其考核评估标准如表:
2016年年底,某商业集团根据相关评分标准,对所属20家商业连锁店进行了年度考核评估,并依据考核评估得分(最低分60分,最高分100分)将这些连锁店分别评定为A,B,C,D四个类型,其考核评估标准如表:| 评估得分 | [60,70) | [70,80) | [80,90) | [90,100] |
| 评分类型 | D | C | B | A |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com