练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设计求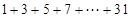的算法，并画出相应的程序框图.

    详见解析.

    解析试题分析：这是一个累加求和的问题，共16项相加，故要设计一个计数变量，一个累加变量，用循环结构实现这一算法，循环变量的初始值为1，终值为31，步长为2，累加变量的初始值为0，由此确定循环前和循环体中各语句，即可得到相应的程序框图.
    试题解析：第一步：；
    第二步：；
    第三步：；
    第四步：；
    第五步：若不大于31，返回执行第三步，否则执行第六步；
    第六步：输出值.
    程序框图如下图：
    .
    考点：1.设计程序框图解决实际问题；2.循环结构.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    执行右边的程序框图,若p＝100，则输出的        

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    执行如图所描述的算法程序,记输出的一列的值依次为,其中且.
    (1)若输入,写出全部输出结果.
    (2)若输入,记,求与的关系().

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    画出解不等式（）的程序框图.

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    有一段演绎推理是这样的：“直线平行于平面，则此直线平行于平面内的所有直线；已知直线平面，直线平面，直线平面，则直线直线”结论显然是错误的，这是因为（   ）

    A．大前提错误 B．推理形式错误 C．小前提错误 D．非以上错误

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

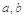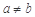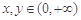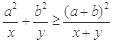    给出命题：若是正常数，且，，则(当且仅当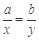时等号成立)．根据上面命题，可以得到函数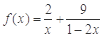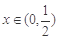（）的最小值及取最小值时的值分别为（   ）

    A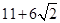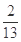．， B．，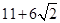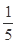
    C．25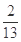， D．，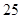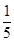

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    用反证法证明命题“三角形的内角至多有一个钝角”时，假设正确的是（ ）

    A．假设至少有一个钝角B．假设至少有两个钝角
    C．假设没有一个钝角D．假设没有一个钝角或至少有两个钝角

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    求和：；试用程序表示．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    用数学归纳法证明“n3＋(n＋1)3＋(n＋2)3(n∈N*)能被9整除”，要利用归纳假设证n＝k＋1时的情况，只需展开(　　)

    A．(k＋3)3 B．(k＋2)3
    C．(k＋1)3 D．(k＋1)3＋(k＋2)3

    查看答案和解析>>

    同步练习册答案